算法设计16——贪婪算法，最小生成树

 

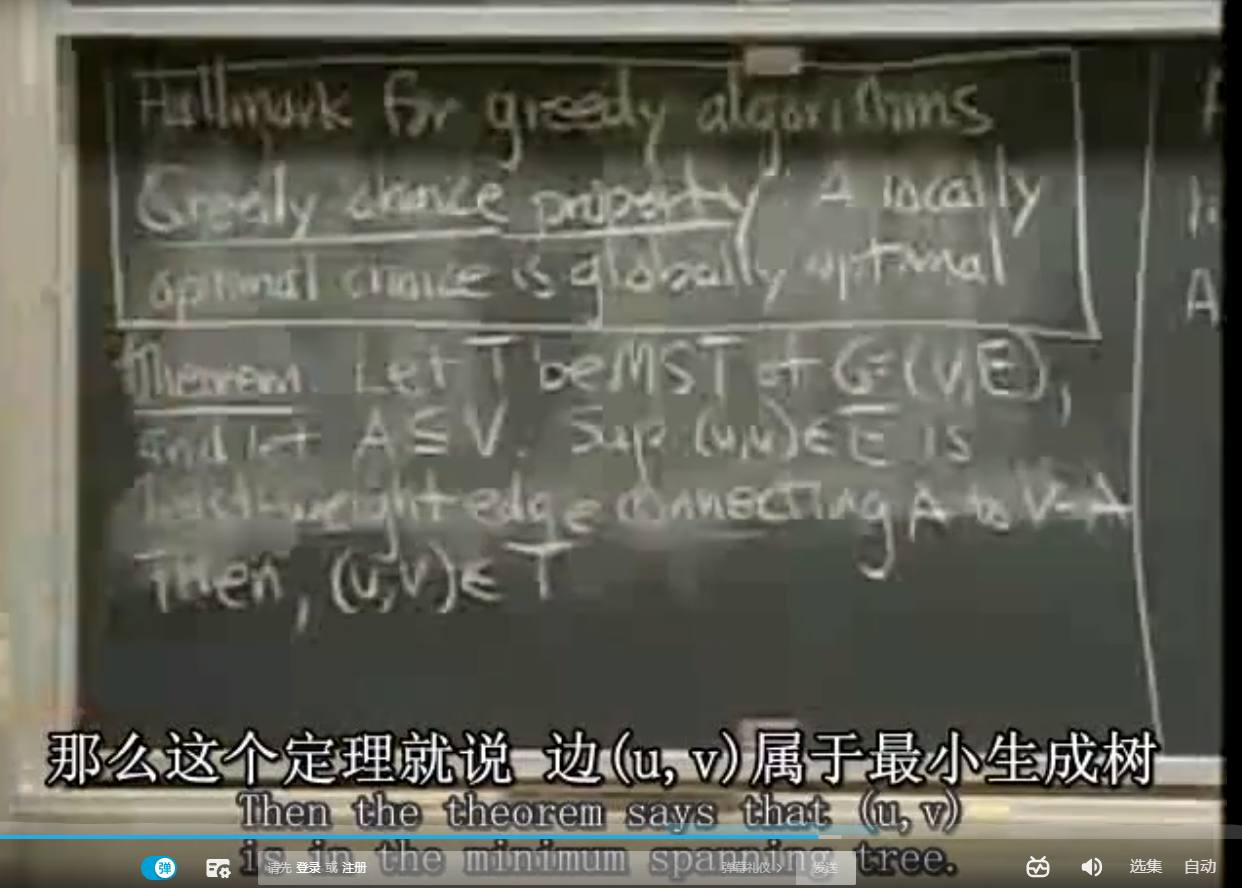
证明：

 使用cut & paste的方式，先假定最小权值边不属于最小生成树，然后先去掉原先连接2棵树的边，连接上最小权值边，会发现新的树权值会更小，证明通过最小权值边一定是属于最小生成树；

关于图的几个概念定义：

• 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
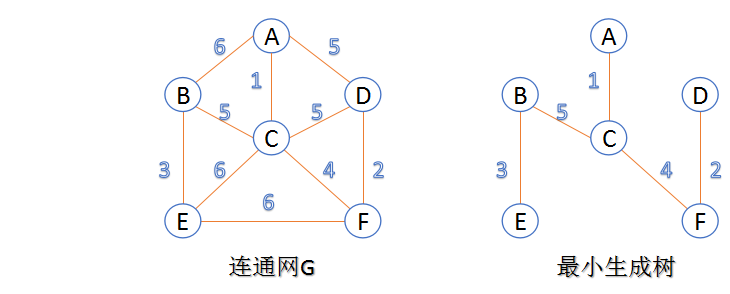
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。 
  

1.Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。 
1. 把图中的所有边按代价从小到大排序； 
2. 把图中的n个顶点看成独立的n棵树组成的森林； 
3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。 
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

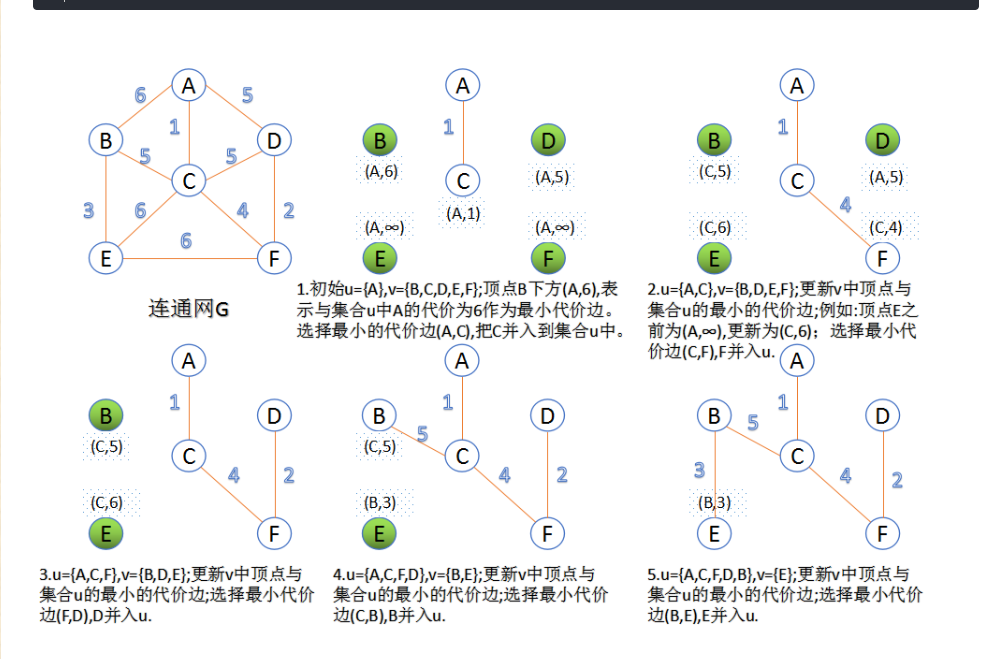
2.Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

伪代码

部分refer：

https://blog.csdn.net/a2392008643/article/details/81781766

开销计算：