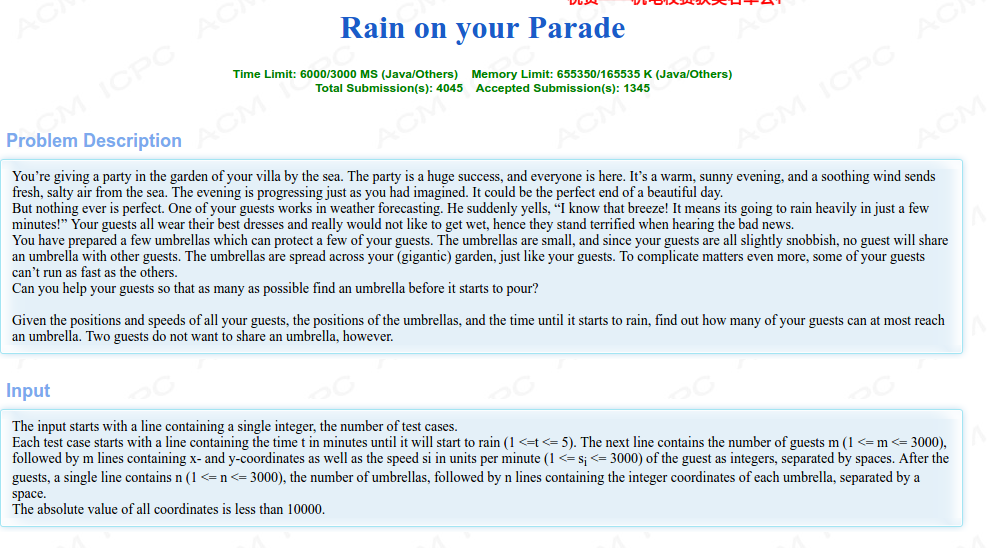
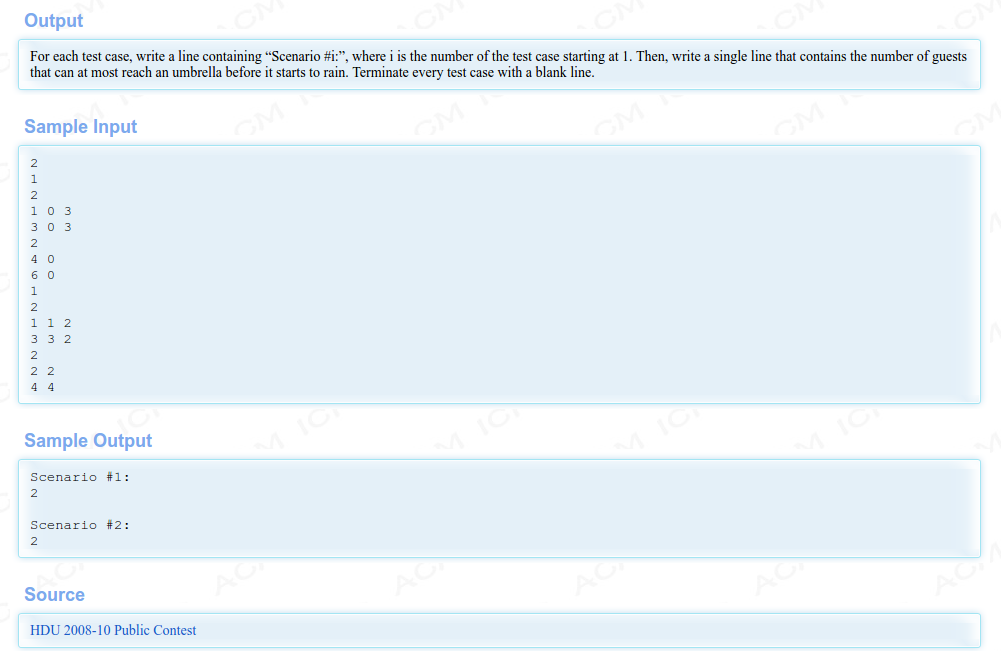
解题思路:
这是一个简单的二分图问题,但是用匈牙利算法,一直TL,后来用Hopcroft-Karp算法过了
实现代码:
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <queue> using namespace std; #define eps 1e-6 const int MAXN=4000; const int INF=1<<30; int map[MAXN][MAXN]; int uN,vN; int cx[MAXN]; int cy[MAXN]; int dx[MAXN]; int dy[MAXN]; int dis; bool bmask[MAXN]; bool searchpath(){ queue<int> Q; dis=INF; memset(dx,-1,sizeof(dx)); memset(dy,-1,sizeof(dy)); for(int i=1;i<=uN;i++){ if(cx[i]==-1) Q.push(i); dx[i]=0; } while(!Q.empty()){ int u=Q.front();Q.pop(); if(dx[u]>dis) break; for(int v=1;v<=vN;v++){ if(map[u][v]&&dy[v]==-1){ dy[v]=dx[u]+1; if(cy[v]==-1) dis=dy[v]; else{ dx[cy[v]]=dy[v]+1; Q.push(cy[v]); } } } } return dis!=INF; } int findpath(int u){ for(int v=1;v<=vN;v++){ if(!bmask[v]&&map[u][v]&&dy[v]==dx[u]+1){ bmask[v]=1; if(cy[v]!=-1&&dy[v]==dis){ continue; } if(cy[v]==-1||findpath(cy[v])){ cy[v]=u; cx[u]=v; return 1; } } } return 0; } int maxMatch(){ int res=0; memset(cx,-1,sizeof(cx)); memset(cy,-1,sizeof(cy)); while(searchpath()){ memset(bmask,0,sizeof(bmask)); for(int i=1;i<=uN;i++){ if(cx[i]==-1) res+=findpath(i); } } return res; } /*int dfs(int u){ for(int i=1;i<=vN;i++){ if(map[u][i]&&!used[i]){ used[i]=true; if(linker[i]==-1||dfs(linker[i])){ linker[i]=u; return 1; } } } return 0; } int maxMatch(){ memset(linker,-1,sizeof(linker)); int res=0; for(int i=1;i<=uN;i++){ memset(used,0,sizeof(used)); res+=dfs(i); } return res; }*/ struct node{ int x,y,t; }guest[MAXN]; struct NN{ int x,y; }MM[MAXN]; double dist(node a,NN b){ double x=a.x-b.x; double y=a.y-b.y; return sqrt(x*x+y*y); } int main(){ int T,iCase=0; scanf("%d",&T); while(T--){ int t; scanf("%d",&t); scanf("%d",&uN); for(int i=1;i<=uN;i++){ scanf("%d%d%d",&guest[i].x,&guest[i].y,&guest[i].t); } scanf("%d",&vN); for(int i=1;i<=vN;i++) scanf("%d%d",&MM[i].x,&MM[i].y); memset(map,0,sizeof(map)); for(int i=1;i<=uN;i++) for(int j=1;j<=vN;j++) if(dist(guest[i],MM[j])/guest[i].t-t<eps) map[i][j]=1; printf("Scenario #%d: %d ",++iCase,maxMatch()); } }