【题目描述】
实现函数 double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同事不需要考虑大数问题。
【解决方案】
1. 自以为题目很简单的解法
1 public static double Power(double baseNum, int exponent) 2 { 3 double result = 1.0; 4 for (int i = 0; i < exponent; i++) 5 { 6 result *= baseNum; 7 } 8 return result; 9 }
2. 全面但不够高效的解法,我们离Offer已经很近了
需要考虑的特殊情况:
a. 底数为0的0次方没有意义,无论输出0还是1都是可以接受的,这需要和面试官说清楚,以证明你考虑到边界值的情况;
b. 指数为负数时,需要先进行乘方,然后求倒;
c. 针对0的负数次方,先乘方,再求倒,会对0求倒,应该针对这种情况做兼容;
d. 错误处理采用什么方式?返回值,全局代码,还是异常?
综合以上特殊情况,可以写出下面代码,仅供参考:
1 public static double Power(double baseNum, int exponent) 2 { 3 double result = 1.0; 4 bool isPositive = true; 5 6 if (Equal(baseNum, 0.0) && (exponent < 0)) 7 { 8 throw new Exception("Invalid Input."); 9 } 10 11 if (exponent < 0) 12 { 13 isPositive = false; 14 exponent = -exponent; 15 } 16 17 result = PowerWithPositiveExponent(baseNum, exponent); 18 19 if (!isPositive) 20 { 21 result = 1.0 / result; 22 } 23 24 return result; 25 } 26 27 public static double PowerWithPositiveExponent(double baseNum, int exponent) 28 { 29 double result = 1.0; 30 31 for (int i = 0; i < exponent; i++) 32 { 33 result *= baseNum; 34 } 35 36 return result; 37 } 38 39 /// <summary> 40 /// 由于计算机表示小数(包括float和double型小数)都有误差, 41 /// 我们不能直接用等号(==)判断两个小数是否相等, 42 /// 如果两个小数的差的绝对值很小,比如小于0.0000001, 43 /// 就可以认为他们相等。 44 /// </summary> 45 /// <param name="num1"></param> 46 /// <param name="num2"></param> 47 /// <returns></returns> 48 public static bool Equal(double num1, double num2) 49 { 50 if ((num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001)) 51 return true; 52 else 53 return false; 54 }
3. 全面又高效的解法,确保我们能拿到Offer
如果面试官对效率要求很高,我们还可以继续优化:
a. 如果exponent为32,则我们需要做32次运算,我们可以换一种思路,如果我们知道了16次方那么只需要计算一次就可以了,想要知道16次方,需要知道8次方。
以此类推,可以得到如下公式,能减少运算的次数,提高效率,代码可以使用递归来实现,
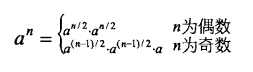
b. 用位运算来替换普通的运算符,效率高很多,既然优化代码,就要把优化做到极致;
我的代码实现,仅供参考:
1 public static double PowerWithPositiveExponent(double baseNum, int exponent) 2 { 3 if (exponent == 0) 4 return 1.0; 5 6 if (exponent == 1) 7 return baseNum; 8 9 double result = PowerWithPositiveExponent(baseNum, exponent >> 1); 10 result *= result; 11 12 if ((exponent & 0x1) == 1) 13 result *= baseNum; 14 15 return result; 16 }