传统的强化学习算法具有很强的决策能力,但难以用于高维空间任务中,需要结合深度学习的高感知能力,因此延展出深度强化学习,最经典的就是DQN(Deep Q-Learning)。
DQN 2013
DQN的主要思想是训练CNN拟合出Q-Learning算法,以此让智能体在复杂的RL环境中从原始视频数据学到成功的控制策略。
实现:
- 用参数( heta)的CNN近似最优Q-values
[Q(s,a; heta)approx Q^*(s,a)
]
- 结合Bellman最优方程得到第(i)次迭代更新的目标
[y_i=mathbb{E}_{s^prime sim mathcal{E}}ig[r+gamma max_{a^prime}Q(s^prime,a^prime; heta_{i-1})|s,aig]
]
- 定义网络的损失函数
[L_i( heta_i)=mathbb{E}_{s,asim
ho(cdot)}ig[ig(y_i-Q(s,a; heta_i) ig)^2ig]$$ $
ho(s,a)$是行为分布(behavior distribution),即在序列$s$上执行动作$a$的概率分布
3. 求出梯度
$$ riangledown_{ heta_i}L_i( heta_i)=mathbb{E}_{s,asim
ho(cdot);s^primesimmathcal{E}}igg[Big(r+gammamax_{a^prime}Q(s^prime,a^prime; heta_{i-1})-Q(s,a; heta_i) Big) riangledown_{ heta_i}Q(s,a; heta_i) igg]]
难点以及解决方法:
- 强化学习假设智能体与环境的交互具有马尔科夫性,而现实中大多任务是部分可观的,智能体很难从当前视频帧(x_t)中获取到足够有用的信息。通过动作和观测序列(s_t=x_1,a_1,x_2,...,a_{t-1},x_t),人为地设定了MDP
- 训练CNN所需的样本需要相互独立,而RL状态间的相关性极高。通过经验回放机制(experience replay mechansim),保存以前的转移并进行随机采样,缓解数据相关性,保证训练数据分布平滑
- 单帧输入不包含时序信息,因此网络输入是经过预处理的4帧堆叠图像
Nature DQN
Nature DQN主要是对DQN 2013做了修改:
- 网络结构
DQN是一个端到端的模型,输入是预处理后的四帧灰度图像的堆叠,先经过三个卷积层提取特征,然后用两个全连接层作为决策层,最后输出为一个向量,向量的元素对应每个可执行动作的概率值,网络结构如下图:
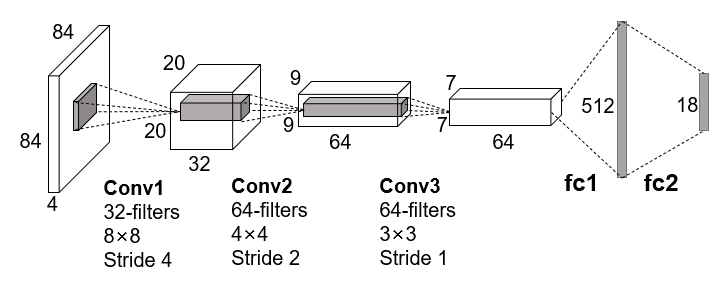
- 减少相关性
DQN 2013的(Q(s,a))和(r+gammamax_{a^prime}Q(s^prime,a^prime))之间存在相关性,因此在网络训练过程中损失难以收敛。为了减少它们的相关性,Nature DQN使用了两个网络:主网络用于模型参数的更新,以及(Q(s,a; heta_i))的拟合;目标网络每隔一个周期对主网络进行一次拷贝,生成近似的目标价值(r+gamma max_{a^prime}Q(s^prime,a^prime; heta_i^-))(( heta_i)是主网络第(i)次迭代的参数,( heta_i^-)是目标网络的参数,是从主网络参数( heta_{i-1})复制得到)。最后,损失函数为
[L_i( heta_i)=mathbb{E}_{(s,a,r,s^prime)sim U(D)}Big[Big(r+gammamax_{a^prime}Q(s^prime,a^prime; heta_i^-)-Q(s,a; heta_i) Big)^2 Big]
]
从而得到梯度:
[ riangledown_{ heta_i}L( heta_i)=mathbb{E}_{s,a,r,s^prime}Big[Big(r+gammamax_{a^prime}Q(s^prime,a^prime; heta_i^-)-Q(s,a; heta_i) Big) riangledown_{ heta_i}Q(s,a; heta_i) Big]
]
其中,(D)是经验回放池,用于存储每一时刻的转移,可以表示为(e_t=(s_t,a_t,r_t,s_{t+1})),(e_tin D_t={e_1,e_2,...,e_t});在学习阶段,用于Q-Learning更新的样本服从于(U(D))分布,即从(D)中均匀采样。从梯度公式中可以看出,只需要更新( heta_i),减小了计算量和相关性。训练过程如下图:
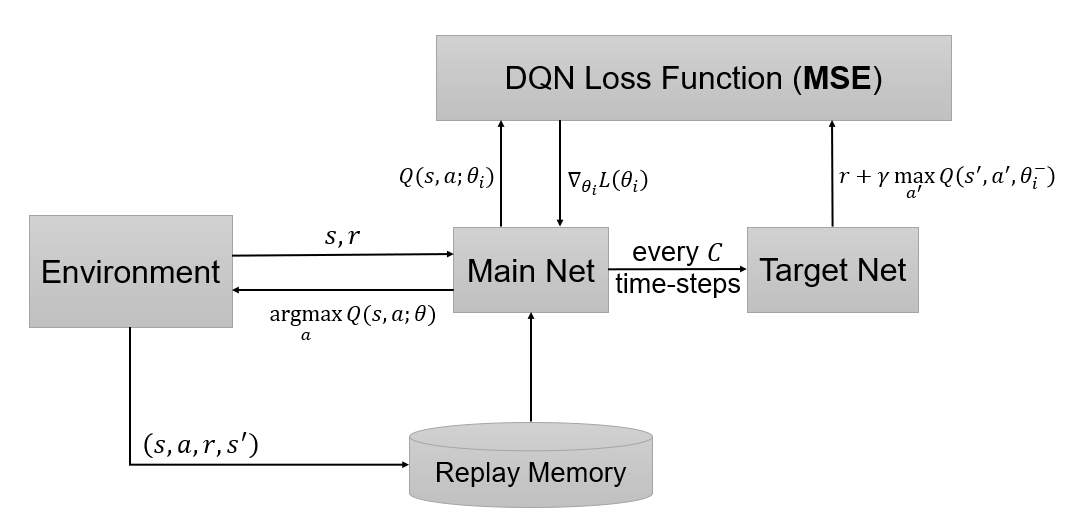
算法伪代码:

References
Volodymyr Mnih et al. Playing Atari with Deep Reinforcement Learning. 2013.
Volodymyr Mnih et al. Human-level control through deep reinforcement learning. 2015.