CodeForces786B 线段树 + 最短路

 

给定n颗行星，q次处理，地球位置为s，求解在q次处理后，地球到每一颗行星的位置。

其中q有三种不同的操作：

 

1. 输入v,u,wv,u,w,构建一条从vv到uu的代价为ww的路线

2. 输入u,l,r,wu,l,r,w，构建一条从uu到区间[l,r][l,r]中任意一颗行星的代价为ww的路线

3. 输入u,l,r,wu,l,r,w，构建区间[l,r]中任意一颗行星到uu的代价为ww的路线

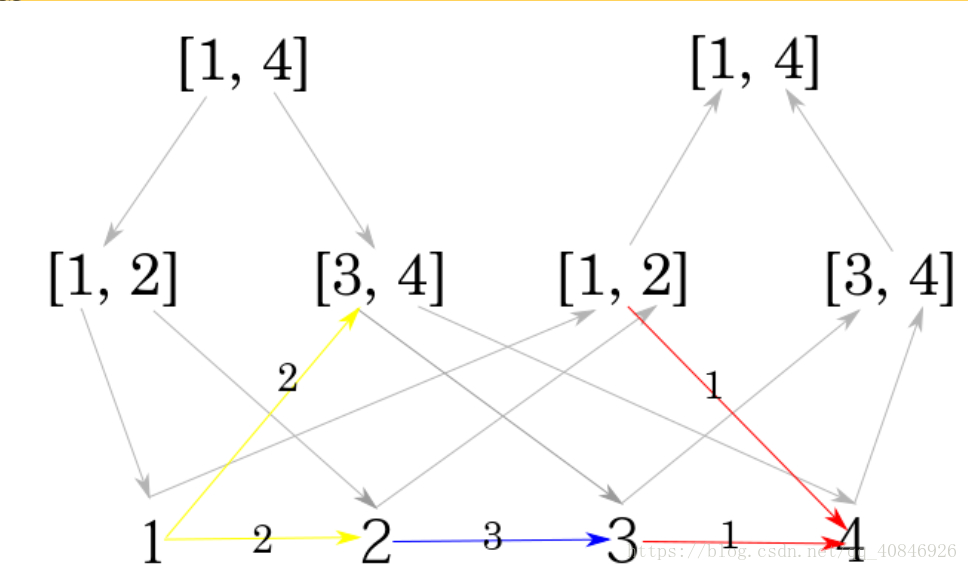
建立两颗线段树，一颗记录操作2中其他点AOE到这些点的区间，一颗记录所有点单独到一个节点的路径，把线段树上的点单独作为一个节点来维护，偷了一个很好的图来表达

 

#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <functional>
#define For(i, x, y) for(int i=x; i<=y; i++)  
#define Mem(f, x) memset(f, x, sizeof(f))  
#define Sca(x) scanf("%d", &x)  
#define Pri(x) printf("%d
", x)  
#define CLR(u) for(int i = 0; i <= N ; i ++) u[i].clear();
#define LL long long  
#define mp make_pair
#define PI pair<int,int>
#define PIL pair<int,long long>
#define PLI pair<long long,int>
#define pb push_back
#define fi first
#define se second 
using namespace std;
typedef vector<int> VI;
const int maxn = 1e5 + 10;
const int maxm = 3e5 + 10;
const LL INF = 1e18 + 10;
const int mod = 1e9 + 7; 
inline int read()
{
    int now=0;register char c=getchar();
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);now=now*10+c-'0',c=getchar());
    return now;
}
struct Tree
{
    int left,right;
    int lr,rr;
}tree[maxm];
int N,M;
int Q,S; 
int tot;
vector<PIL> P[maxm];
LL dis[maxm];
bool vis[maxm]; 
int Build(int left,int right,int flag)
{
    if(left == right) return left;
    int root = ++tot;
    tree[root].left = left; tree[root].right = right;
    int mid = (left + right) / 2;
    tree[root].lr = Build(left,mid,flag);
    tree[root].rr = Build(mid + 1,right,flag);
    if(flag){
        P[root].pb(mp(tree[root].lr,0));
        P[root].pb(mp(tree[root].rr,0));
    }else{
        P[tree[root].lr].pb(mp(root,0));
        P[tree[root].rr].pb(mp(root,0));
    }
    return root;
}
void update(int v,int l,int r,int root,int flag,LL w)
{
    if(l == r){
        if(flag) P[v].pb(mp(l,w));
        else P[l].pb(mp(v,w));
        return;
    }
    if(l <= tree[root].left && tree[root].right <= r)
    {
        if(flag) P[v].pb(mp(root,w));
        else P[root].pb(mp(v,w));
        return;
    }
    int mid = (tree[root].left + tree[root].right) >> 1;
    if(r <= mid) update(v,l,r,tree[root].lr,flag,w);
    else if(l > mid) update(v,l,r,tree[root].rr,flag,w);
    else{
        update(v,l,mid,tree[root].lr,flag,w);
        update(v,mid + 1,r,tree[root].rr,flag,w);
    }
    
}
void Dijkstra(int start){
    Mem(vis,0);
    for(int i = 1; i <= tot; i ++){
        dis[i] = INF;
    }
    dis[start] = 0;
    priority_queue<PLI,vector<PLI>,greater<PLI>>Q;
    Q.push(mp(0,start));
    while(!Q.empty()){
        PLI u = Q.top(); Q.pop();
        if(vis[u.se]) continue;
        vis[u.se] = 1;
        for(int j = 0 ; j < P[u.se].size(); j ++){
            PIL v = P[u.se][j];
            if(!vis[v.fi] && dis[v.fi] > dis[u.se] + v.se){
                dis[v.fi] = dis[u.se] + v.se;
                Q.push(mp(dis[v.fi],v.fi));
            }
        }
    }
}
 
int main()
{
    N = read(); Q = read(); S = read();
    tot = N;
    int L = Build(1,N,0);
    int R = Build(1,N,1);
    For(i,1,Q){
        int op = read() , v = read();
        LL w;
        if(op == 1){
            int u = read();
            scanf("%lld",&w);
            P[v].pb(mp(u,w));
        }else if(op == 2){
            int l = read(); int r = read();
            scanf("%lld",&w);
            update(v,l,r,R,1,w);
        }else{
            int l = read(); int r = read();
            scanf("%lld",&w);
            update(v,l,r,L,0,w);
        }
    }
/*    For(i,N + 1,tot){
    printf("%d   : %d %d
",i,tree[i].left,tree[i].right);
    }
    For(i,1,tot){
        printf("%d : ",i);
        for(int j = 0 ; j < P[i].size(); j ++){
            printf("%d ",P[i][j]);
        }
        printf("
");
    } */
    Dijkstra(S);
    For(i,1,N){
        if(dis[i] == INF) dis[i] = -1;
        printf("%lld ",dis[i]);
    }
    return 0;
}