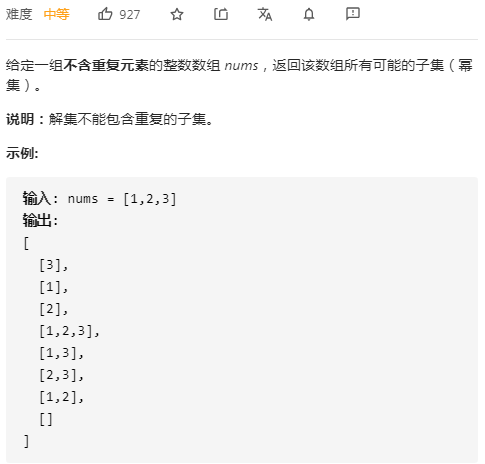
☆☆☆思路:回溯算法。注意对比区分这三道题:求排列、求组合、求子集。
求组合 和 求子集 方法的对比:
更新res的位置不同:求组合时,res 的更新是当树到达底端时;而求子集,res的更新是树上每一个节点,走过的路径都是子集的一部分。
求组合 和 求排列 方法的对比:
树的形状不同:排列问题的树比较对称,而组合问题的树越靠右节点越少。
是否讲究顺序:组合问题不讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表),需要按照某种顺序搜索。而排列问题,讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表),需要记录那些数字已经使用过。
代码中的体现:组合问题从当前位置往后搜索,排除了当前位置之前的数字。而排列问题每次都需要从头寻找,需要用vis数组记录访问过的元素。
代码1(回溯常规写法):
class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res = new ArrayList<>(); dfs(nums, 0, new ArrayList<>(), res); return res; } // 以[1,2,3]为例,搜索添加顺序为 // [[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]] private void dfs(int[] nums, int start, List<Integer> list, List<List<Integer>> res) { // 走过的所有路径都是子集的一部分,所以都要加入到集合中 res.add(new ArrayList<>(list)); for (int i = start; i < nums.length; i++) { list.add(nums[i]); dfs(nums, i + 1, list, res); list.remove(list.size() - 1); } } }
代码2(回溯做选择):
class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res = new ArrayList<>(); dfs(nums, 0, new ArrayList<>(), res); return res; } // 以[1,2,3]为例,搜索添加顺序为 // [ [1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[] ] private void dfs(int[] nums, int index, List<Integer> list, List<List<Integer>> res) { if (index == nums.length) { res.add(new ArrayList<>(list)); return; } // 选择当前位置 list.add(nums[index]); dfs(nums, index + 1, list, res); list.remove(list.size() - 1); // 不选择当前位置 dfs(nums, index + 1, list, res); } }