先来回顾一下什么是梯度：
对多元函数的参数求偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度 。
接下来看一下什么是导数和偏导数：
我们知道，函数在某一点的导数就是该函数所代表的曲线在这一点上的变化率。而偏导数涉及到至少两个自变量，因此，从导数到偏导数，就是从曲线变成了曲面。曲线上某一点的切线只有一条，但是曲面上某一点的切线却有无数条。
这就牵出了方向导数的概念：如果函数f在某点(x,y)是可微分的，那么函数在该点沿任一方向的方向导数都存在，且有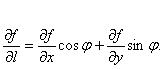
（其中l为轴到方向的转角）。这就是说，函数在曲面上某点的变化率是有方向的。
那么，为什么说梯度指向函数上升最快的方向呢？答案是：这就是梯度的定义。
首先来证明方向导数：
假设函数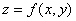
在点
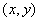可微分，那么函数的增量可以表达为：
，
两边各除以ρ，得到：
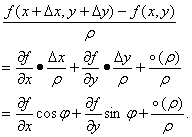
所以：
这就证明了方向导数存在且其值为。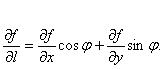
令向量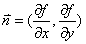
，方向l的向量为
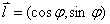，因此：
。当n与l同向时，便能取得最大的方向导数，我们称n为f在该点的梯度。方向导数最大，也就是说n的模最大，函数f朝l方向的变化率最大。因此，从几何意义上讲，梯度指向函数增加最快的方向。
总结来说：函数在某点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。