因为光看模型在训练集上的表现容易导致过拟合,因此回归模型通常有两种评价方式,一种是看验证/交叉验证的结果,另一种是对训练集上的表现结果进行修正,常见指标有:AIC,BIC,Cp,adjusted R2。
用验证/交叉验证方式评价回归模型性能的指标(Performance Evaluation Metric)通常有:
1. 平均绝对误差(Mean Absolute Error, MAE):真实目标y与估计值y-hat之间差值的平均值

(注:m为测试集样本数量,下同)
2. 均方误差(Mean Squared Error, MSE):真实目标y与估计值y-hat之间差值的平方的平均值
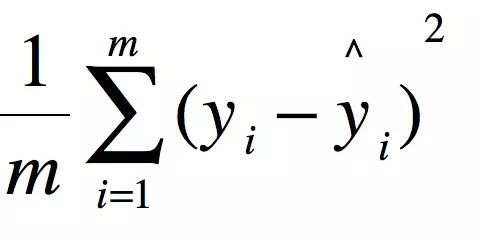
对比平均绝对误差,均方误差对异常值更敏感。
3. 均方根误差(Root Mean Squared Error, RMSE):均方误差的方根,可从单位度量上衡量模型的效果
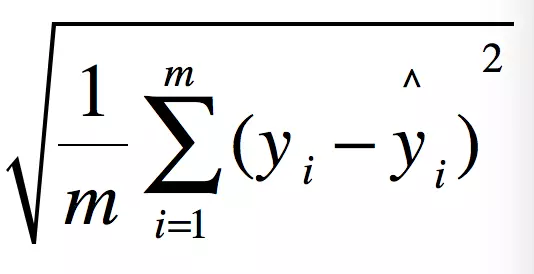
上述几个验证误差或交叉验证误差越小,就代表模型的性能越好。
下面再说一下R2和adjusted R2:
决定系数(Coefficient of Determination)R2:目标的变化由特征引起的比例
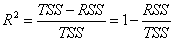
R2的值是多少代表模型的性能好?谁也不知道。有的例子中,只要R2达到0.5-0.6就已经很好了。此外,从理论上来说,只要增加特征的个数,R2的值是一直增加的,不管这个特征x和目标y是否有关。因此,R2通常用于特征选择。如果增加一个特征,模型的R2值上升很多,那就说明这个特征和目标有关。
adjusted R2:与R2类似,不过增加了惩罚项,因此adjusted R2一定小于等于R2。如果新增的特征没有带来任何有用的信息,那么adjusted R2会变小,只有在新增的特征带来足够多的信息(足够抵消惩罚项)时,adjusted R2才会增加。其缺点是无法像R2一样对模型进行解释。
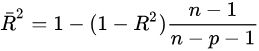
如果以R2为评价指标,容易让模型出现过拟合现象,因此建议用调整的R2(adjusted R-squared)来选择模型,用R2来解释模型。