1、
随意组合
小明被绑架到X星球的巫师W那里。
其时,W正在玩弄两组数据 (2 3 5 8) 和 (1 4 6 7)
他命令小明从一组数据中分别取数与另一组中的数配对,共配成4对(组中的每个数必被用到)。
小明的配法是:{(8,7),(5,6),(3,4),(2,1)}
巫师凝视片刻,突然说这个配法太棒了!
因为:
每个配对中的数字组成两位数,求平方和,无论正倒,居然相等:
87^2 + 56^2 + 34^2 + 21^2 = 12302
78^2 + 65^2 + 43^2 + 12^2 = 12302
小明想了想说:“这有什么奇怪呢,我们地球人都知道,随便配配也可以啊!”
{(8,6),(5,4),(3,1),(2,7)}
86^2 + 54^2 + 31^2 + 27^2 = 12002
68^2 + 45^2 + 13^2 + 7
2^2 = 12002
巫师顿时凌乱了。。。。。
请你计算一下,包括上边给出的两种配法,巫师的两组数据一共有多少种配对方案具有该特征。
配对方案计数时,不考虑配对的出现次序。
就是说:
{(8,7),(5,6),(3,4),(2,1)}
与
{(5,6),(8,7),(3,4),(2,1)}
是同一种方案。
注意:需要提交的是一个整数,不要填写任何多余内容(比如,解释说明文字等)
//随意组合 --- 一
//组合数:n*f(n-1) == f(1) = 1;f(2) = 2; f(3) = 6;f(4) = 24;
#include<stdio.h>
int f(int n){
if(n==1)
return 1;
else{
return n*f(n-1);
}
}
int main(){
int n = 4,num = 0;
num = f(n);
printf("%d",num);
return 0;
}
//
#include<stdio.h> int a[4] = {2,3,5,8},b[4] = {1,4,6,7}; int x[4],y[4],check[4]; int ans = 0; void fun(int n){ int i; if(n==4){ int sum1 = 0,sum2 = 0; for(i=0;i<4;i++){ sum1 += x[i]*x[i]; sum2 += y[i]*y[i]; } if(sum1 == sum2) ans++; return; } for(i=0;i<4;i++){ if(check[i] == 0){ check[i] = 1; x[n] = a[n]*10 + b[i]; y[n] = b[i]*10 + a[n]; fun(n+1); check[i] = 0; } } } int main(){ fun(0); printf("%d",ans); return 0; }
2、
拼棋盘
有 8x8 和 6x6 的棋盘两块(棋盘厚度相同,单面有棋盘,背面无图案)。参见【图1.png】
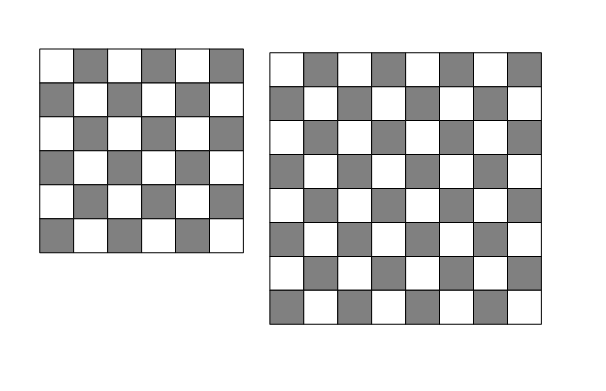
组成棋盘的小格子是同样大小的正方形,黑白间错排列。
现在需要一个10x10的大棋盘,希望能通过锯开这两个棋盘,重新组合出大棋盘。
要求:
1。 拼好的大棋盘仍然保持黑白格间错的特性。
2。 两个已有的棋盘都只允许锯一锯(即锯开为两块),必须沿着小格的边沿,可以折线锯开。
3。 要尽量保证8x8棋盘的完整,也就是说,从它上边锯下的那块的面积要尽可能小。
要求提交的数据是:4块锯好的部分的面积。按从小到大排列,用空格分开。
(约定每个小格的面积为1)
比如:10 10 26 54
当然,这个不是正确答案。
请严格按要求格式提交数据,不要填写任何多余的内容(比如,说明解释等)
3、
打靶
小明参加X星球的打靶比赛。
比赛使用电子感应计分系统。其中有一局,小明得了96分。
这局小明共打了6发子弹,没有脱靶。
但望远镜看过去,只有3个弹孔。
显然,有些子弹准确地穿过了前边的弹孔。
不同环数得分是这样设置的:
1,2,3,5,10,20,25,50
那么小明的6发子弹得分都是多少呢?有哪些可能情况呢?
下面的程序解决了这个问题。
仔细阅读分析代码,填写划线部分缺失的内容。
#include <stdio.h>
#define N 8
void f(int ta[], int da[], int k, int ho, int bu, int sc)
{ //k: ho:弹孔数 bu:子弹数 sc:得分数
int i,j;
if(ho<0 || bu<0 || sc<0)
return;
if(k==N){
if(ho>0 || bu>0 || sc>0)
return;
for(i=0; i<N; i++){
for(j=0; j<da[i]; j++)
printf("%d ", ta[i]);
}
printf("
");
return;
}
for(i=0; i<=bu; i++){
da[k] = i;
f(ta, da, k+1, i>0?ho-1:ho,/*_____________ ,*/bu-i, sc-ta[k]*i); //填空位置
}
da[k] = 0;
}
int main()
{
int ta[] = {1,2,3,5,10,20,25,50}; //对应环数的得分
int da[N];
f(ta, da, 0, 3, 6, 96);
return 0;
}
注意:只填写划线处缺少的内容,不要填写已有的代码或符号,也不要填写任何解释说明文字等。
4、
路径之谜
小明冒充X星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n x n 个方格。【如图1.png】所示。

按习俗,骑士要从西北角走到东南角。
可以横向或纵向移动,但不能斜着走,也不能跳跃。
每走到一个新方格,就要向正北方和正西方各射一箭。
(城堡的西墙和北墙内各有 n 个靶子)
同一个方格只允许经过一次。但不必走完所有的方格。
如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?
有时是可以的,比如图1.png中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入:
第一行一个整数N(0<N<20),表示地面有 N x N 个方格
第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出:
一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3....
比如,图1.png中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
示例:
用户输入:
4
2 4 3 4
4 3 3 3
程序应该输出:
0 4 5 1 2 3 7 11 10 9 13 14 15
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
5、
碱基
生物学家正在对n个物种进行研究。
其中第i个物种的DNA序列为s[i],其中的第j个碱基为s[i][j],碱基一定是A、T、G、C之一。
生物学家想找到这些生物中一部分生物的一些共性,他们现在关注那些至少在m个生物中出现的长度为k的连续碱基序列。准确的说,科学家关心的序列用2m元组(i1,p1,i2,p2....im,pm)表示,
满足:
1<=i1<i2<....<im<=n;
且对于所有q(0<=q<k), s[i1][p1+q]=s[i2][p2+q]=....=s[im][pm+q]。
现在给定所有生物的DNA序列,请告诉科学家有多少的2m元组是需要关注的。如果两个2m元组有任何一个位置不同,则认为是不同的元组。
【输入格式】
输入的第一行包含三个整数n、m、k,两个整数之间用一个空格分隔,意义如题目所述。
接下来n行,每行一个字符串表示一种生物的DNA序列。
DNA序列从1至n编号,每个序列中的碱基从1开始依次编号,不同的生物的DNA序列长度可能不同。
【输出格式】
输出一个整数,表示关注的元组个数。
答案可能很大,你需要输出答案除以1000000007的余数。
【样例输入】
3 2 2
ATC
TCG
ACG
【样例输出】
2
再例如:
【样例输入】
4 3 3
AAA
AAAA
AAA
AAA
【样例输出】
7
【数据规模与约定】
对于20%的数据,k<=5,所有字符串总长L满足L <=100
对于30%的数据,L<=10000
对于60%的数据,L<=30000
对于100%的数据,n<=5,m<=5,1<=k<=L<=100000
保证所有DNA序列不为空且只会包含’A’ ’G’ ’C’ ’T’四种字母
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
6、
圆圈舞
春天温暖的阳光照耀着大地,正是草原上的小动物们最快乐的时候。小动物们在草原上开了一个舞会,欢度这美好的时光。
舞会上最重要的一个环节就是跳圆舞曲,n只小动物手拉手围成一大圈,随着音乐跳起来。在跳的过程中,小动物们可能会变换队形。它们的变换方式是动物A松开自己右手,动物B松开自己的左手,动物A和B手拉到一起,而它们对应的松开的手(如果有的话)也拉到一起。
例如,假设有10只小动物,按顺序围成一圈,动物1的右手拉着动物2的左手,动物2的右手拉着动物3的左手,依次类推,最后动物10的右手拉着动物1的左手。如果通过动物2和8变换队形,则动物2的右手拉着动物8的左手,而对应的动物3的左手拉着动物7的右手,这样形成了1-2-8-9-10和3-4-5-6-7两个圈。如果此时通过动物2和6变换队形,则将形成1-2-6-7-3-4-5-8-9-10一个大圈。注意,如果此时通过动物1和2变换队形,那么队形不会改变,因为动物1的右手和动物2的左手松开后又拉到一起了。
在跳舞的过程中,每个动物i都有一个欢乐值Hi和一个感动值Fi。
如果两个动物在一个圈中,欢乐值会彼此影响,产生欢乐能量。如果两个动物i, j(i≠j)在同一个大小为t的圈中,而动物i在动物j右手的第p个位置(动物j右手的第1个位置就是动物j右手所拉着的动物,而第2个位置就是右手第1个位置的动物右手拉着的动物,依次类推),则产生的欢乐能量为(t-p)*Hj*Fi。在跳舞的过程中,动物们的欢乐值和感动值有可能发生变化。
圆舞曲开始的时候,所有的动物按编号顺序围成一个圈,动物n右手的第i个位置正好是动物i。现在已知小动物们变换队形的过程和欢乐值、感动值变化的过程,求每次变换后所有动物所产生的欢迎能量之和。
【输入格式】
输入的第一行包含一个整数n,表示动物的数量。
接下来n行,每行两个用空格分隔的整数Hi, Fi,按编号顺序给出每只动物的欢乐值和感动值。
接下来一行包含一个整数m,表示队形、欢乐值、感动值的变化次数。
接下来m行,每行三个用空格分隔的整数k, p, q,当k=1时,表示小动物们通过动物p和动物q变换了队形,当k=2时,表示动物p的欢乐值变为q,当k=3时,表示动物p的感动值变为了q。
【输出格式】
输出m行,每行一个整数,表示每次变化后所有动物产生的能量之和。
答案可能很大,你需要计算答案除以1000000007的余数。
【样例输入】
10
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
9
1 2 8
1 2 6
2 8 10
3 5 10
1 1 2
1 2 1
2 5 5
1 4 8
1 4 5
【样例输出】
100
450
855
1341
1341
811
923
338
923
【数据规模与约定】
对于20%的数据,2<=n,m<=100。
对于30%的数据,2<=n,m<=1000。
另有20%的数据,只有k=1的操作且Hi,Fi均为1。
另有20%的数据,只有k=1或2的操作且Fi均为1。
对于100%的数据,2<=n,m<=100000,0<=Hi,Fi<=10^9,1<=k<=3,k=1时1<=p,q<=n且p≠q,k=2或3时1<=p<=n且0<=q<=10^9。
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2500ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。