小根堆的Java实现

---

1. 堆

堆是完全二叉树的数组形式，由于堆没有指针指向，所以可以利用下标来模拟指向，假设 i 为父节点，那么 2i+1 为左孩子，2i+2 为右孩子。假设 i 为当前节点，那么 (i - 1) / 2 为父节点

根据大小排序可分为小根堆和大根堆，小根堆即元素越小越在上方，大根堆则相反。这里注意：元素大小并不是按数组下标来排序的，下图的数字对应数组的坐标

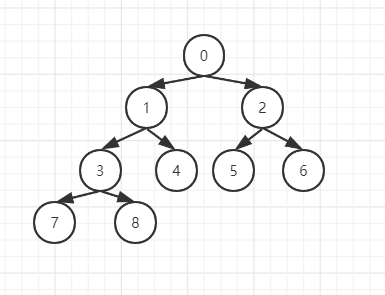
堆的应用：

• 堆排序
• 优先级队列
• 快速找最值

2. 小根堆实现

内部操作有：

• 上浮：将小的元素往上移动、当插入元素时，将元素插入末尾，这样上移即可调整位置
• 下沉：将大的元素向下移动、当删除元素时，将首位交换，弹出尾部，首部下移即可调整位置
• 插入：添加元素
• 弹出：删除元素

主要是其插入弹出的思想，还有调整时注意下标，因为大小与下标相差1

package heap;

// 小根堆时间复杂度是O(1) ~ O(logn)
// 默认O(nlogn)
public class Heap {

    // 实际存放元素个数
    // 这里是个坑，debug了好久，起因：下标 = 实际大小-1
    private int size;

    // 数组存储元素
    // 可以实现简单扩容，size++ > capacity时
    // data = copyOf(data,capacity*2);
    private int[] data = new int[10];

    // 交换，传入下标
    private void swap(int a, int b) {
        int temp = data[a];
        data[a] = data[b];
        data[b] = temp;
    }

    // 较大的下沉
    // 将当前节点与其较小儿子交换
    // 并将更新当前节点为交换的儿子节点
    public void fixDown(int index) {
        int son = index * 2 + 1;
        while (son <= size) {
            if (son + 1 < size && data[son + 1] < data[son]) {
                son++;  // 这里这要比较左右孩子谁小
            }
            if (data[index] < data[son]) {
                break;  // 当前节点比孩子节点小，不用下沉退出循环
            } else {
                swap(index, son);
                index = son;
                son = index * 2 + 1;
            }
        }
    }

    // 较小的上浮
    // 当前节点与父节点相比，若小于则交换，且将当前节点跟新为其父节点
    public void fixUp(int index) {
        int father = (index - 1) / 2;
        while (father >= 0) {
            // 这里卡死一次，debug后发现，只有一个元素会相等进入无限交换
            if (data[index] >= data[father]) {
                break;  // 其父节点大于当前节点，不用上浮退出循环
            } else {
                swap(index, father);
                index = father;
                father = (index - 1) / 2;
            }
        }
    }

    // 插入
    // 每次都在最后一个插入，然后上浮到合适位置
    public Heap push(int value) {
        data[size] = value;
        fixUp(size++);
        return this;
    }

    // 弹出根元素
    // 让根元素和尾元素交换，让现在的根元素下沉即可
    public int pop() {
        swap(0, --size);
        fixDown(0);
        return data[size];
    }

    // 测试
    public static void main(String[] args) {
        Heap heap = new Heap();

        // 乱序添加1~9
        // 从输出也可以验证，元素大小并不是按数组小标来排序的
        // 输出：123459786
        heap.push(8).push(5).push(9)
                .push(4).push(2).push(3)
                .push(6).push(7).push(1);
        while(heap.size > 0){
            System.out.print(heap.pop());
        }
    }
}