1)Github项目地址:
the address of github
2)PSP 2.1表格:
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 40 |
| · Estimate | · 估计这个任务需要多少时间 | 120 | 180 |
| Development | 开发 | 300 | 360 |
| · Analysis | · 需求分析 (包括学习新技术) | 20 | 30 |
| · Design Spec | · 生成设计文档 | 10 | 15 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 45 | 50 |
| · Coding | · 具体编码 | 60 | 120 |
| · Code Review | · 代码复审 | 60 | 80 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 40 | 60 |
| Reporting | 报告 | 40 | 70 |
| · Test Report | · 测试报告 | 40 | 60 |
| · Size Measurement | · 计算工作量 | 5 | 8 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 40 |
| 合计 | 830 | 1153 |
3)解决思路描述:
- ①首先,任务描述为:
用程序随机构造出N个已解答的数独棋盘。(根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复。)
根据这个条件的话感觉很简单,即构造一个9*9数组,并根据对应的三个条件确定每个位置上要填的数字。
- ②因为有新增要求如下
2017.9.4 新增要求] 在生成数独矩阵时,左上角的第一个数为:(学号后两位相加)% 9 + 1
所以改变思路,先满足第一行第一个数,再去随机生成其他数字。
4)设计实现过程:
- ①初始化一个9*9数组,每个位置都为0,[0][0]位置置为要求的数字。
- ②先随机生成第一行。
- ③从第二行第一个位置开始迭代,根据对应的三个条件确定数字。
- ④未找到满足条件的数字时,回溯到前一个位置并重新填数。(重点)
5)代码说明:
- ①随机生成第一行及判断输入
int main(int argc,char* argv[])
{
string ss = argv[2];
int len = ss.length();
for (int i = 0; i < len;i++) {
if (ss[i]<'0' || ss[i]>'9') {
printf("error input");
return 0;
}
else {
N = N * 10 + ss[i] - '0';
}
}
freopen("sudoku.txt","w",stdout);
srand((unsigned)time(NULL));
sudoku[0][0] = 9;
for (int i = 1; i<9; i++)
{
sudoku[0][i] = i;
}
random_shuffle(&(sudoku[0][1]), &(sudoku[0][8]));
produce_sudoku(1, 0, 1);
return 0;
}
- ②判断是否满足条件
bool judge(int line,int column,int a,int sudoku[9][9])
{
int x,y;
for(int i=0; i<9; i++)//行判断
{
if(sudoku[line][i]==a)
{
return false;
}
}
for(int i=0; i<9; i++)//列判断
{
if(sudoku[i][column]==a)
{
return false;
}
}
x = (line/3)*3;
y = (column/3)*3;
for(int i=x; i<x+3; i++)//九宫格判断
{
for(int j=y; j<y+3; j++)
{
if(sudoku[i][j]==a)
{
return false;
}
}
}
return true;
}
- ③依次判断及回溯
void produce_sudoku(int i,int j,int z)
{
if (j < 0)
{
i--;
j=0;
}
if(j>8)//换行
{
i++;
j=0;
}
if(i==9&&j==0)
{
for(int k=0; k<9; k++)
{
for(int l=0; l<9; l++)
{
cout << sudoku[k][l] << " ";
}
cout << endl;
}
cout<<endl;
if (--N <= 0)
{
exit(0);
}
}
else if (i < 9) //z的作用为防止生成重复矩阵
{
for(int kk=1;kk<9;kk++){
int n = (z++)%9 + 1;
if(judge(i,j,n,sudoku))
{
sudoku[i][j] = n;
produce_sudoku(i,j+1,z);//----回溯 ----
sudoku[i][j] =0;//----回溯 ----
}
}
}
}
6)测试运行(DEV)
-
①N=1000:

-
②N=10000:

7)效能分析(100W):
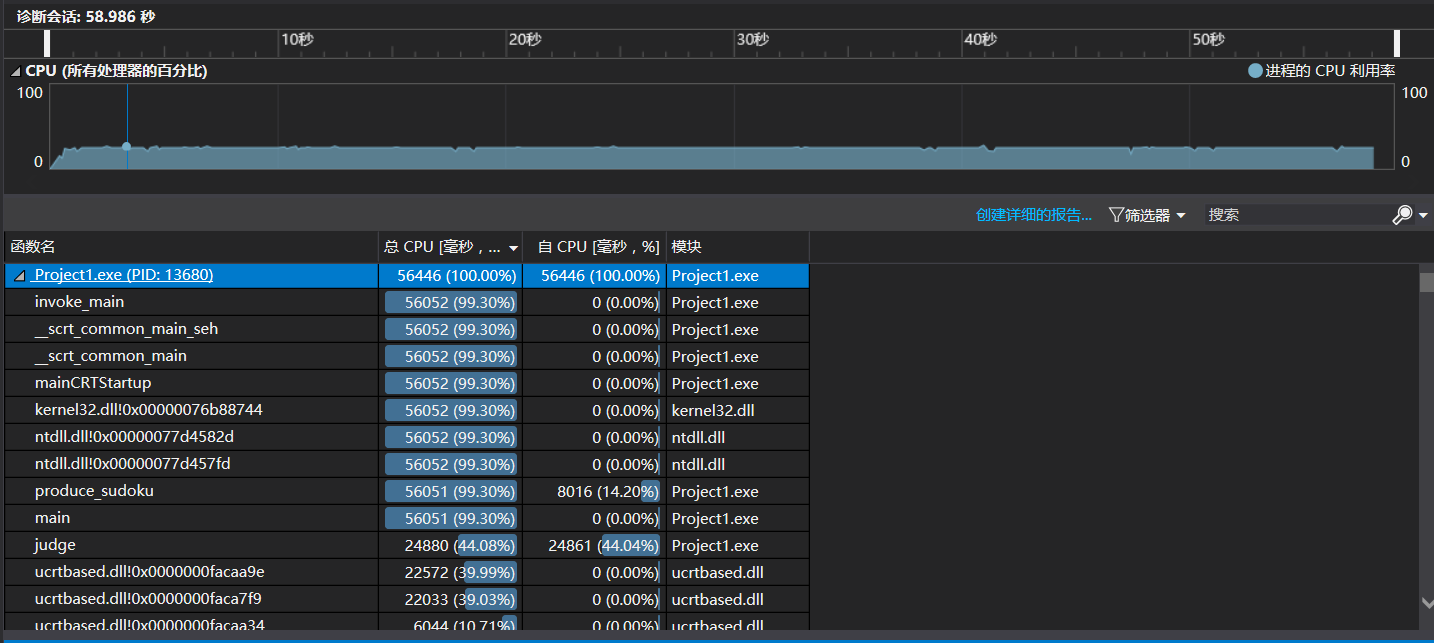
报告分析:
时长主要耗在produce_sudoku函数中的回溯过程,代码执行效率和算法有待提高。