链接:http://blog.csdn.net/morewindows/article/details/6668714
希尔排序的实质就是分组插入排序,该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
以n=10的一个数组49, 38, 65, 97, 26, 13, 27, 49, 55, 4为例
第一次 gap = 10 / 2 = 5
49 38 65 97 26 13 27 49 55 4
1A 1B
2A 2B
3A 3B
4A 4B
5A 5B
1A,1B,2A,2B等为分组标记,数字相同的表示在同一组,大写字母表示是该组的第几个元素, 每次对同一组的数据进行直接插入排序。即分成了五组(49, 13) (38, 27) (65, 49) (97, 55) (26, 4)这样每组排序后就变成了(13, 49) (27, 38) (49, 65) (55, 97) (4, 26),下同。
排序结果为:13 27 49 55 4 49 38 65 97 26
第二次 gap = 5 / 2 = 3
排序后
13 27 49 55 4 49 38 65 97 26
1A 1B 1C 1D 1E
2A 2B 2C 2D 2E
第三次 gap = 3 / 2 = 1
4 26 13 27 38 49 49 55 97 65
1A 1B 1C 1D 1E 1F 1G 1H 1I 1J
第四次 gap = 1 / 2 = 0 排序完成得到数组:
4 13 26 27 38 49 49 55 65 97
下面给出严格按照定义来写的希尔排序
void shellsort1(int a[], int n) { int i, j, gap; for (gap = n / 2; gap > 0; gap /= 2) //步长 for (i = 0; i < gap; i++) //直接插入排序 { for (j = i + gap; j < n; j += gap) if (a[j] < a[j - gap]) { int temp = a[j]; int k = j - gap; while (k >= 0 && a[k] > temp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = temp; } } }
很明显,上面的shellsort1代码虽然对直观的理解希尔排序有帮助,但代码量太大了,不够简洁清晰。因此进行下改进和优化,以第二次排序为例,原来是每次从1A到1E,从2A到2E,可以改成从1B开始,先和1A比较,然后取2B与2A比较,再取1C与前面自己组内的数据比较…….。这种每次从数组第gap个元素开始,每个元素与自己组内的数据进行直接插入排序显然也是正确的。
void shellsort2(int a[], int n) { int j, gap; for (gap = n / 2; gap > 0; gap /= 2) for (j = gap; j < n; j++)//从数组第gap个元素开始 if (a[j] < a[j - gap])//每个元素与自己组内的数据进行直接插入排序 { int temp = a[j]; int k = j - gap; while (k >= 0 && a[k] > temp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = temp; } }
再将直接插入排序部分用 白话经典算法系列之二 直接插入排序的三种实现 中直接插入排序的第三种方法来改写下:
void shellsort3(int a[], int n) { int i, j, gap; for (gap = n / 2; gap > 0; gap /= 2) for (i = gap; i < n; i++) for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap) Swap(a[j], a[j + gap]); }
这样代码就变得非常简洁了。
附注:上面希尔排序的步长选择都是从n/2开始,每次再减半,直到最后为1。其实也可以有另外的更高效的步长选择,如果读者有兴趣了解,请参阅维基百科上对希尔排序步长的说明:http://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F
补充步长选择:
已知的最好步长串行是由Sedgewick提出的 (1, 5, 19, 41, 109,...),该串行的项来自 9 * 4^i - 9 * 2^i + 1 和 4^i - 3 * 2^i + 1 这两个算式[1].这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长串行的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
另一个在大数组中表现优异的步长串行是(斐波那契数列除去0和1将剩余的数以黄金分区比的两倍的幂进行运算得到的数列):(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713, …)[2]
补充下复杂度情况:
| 步长串行 | 最坏情况下复杂度 |
|---|---|
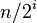 |
 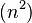 |
 |
  |
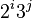 |
 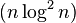 |
(摘自维基百科)
说明:
为了让更多的人看得懂,我补充图形如下,参考:http://blog.163.com/pinbo_jiankun/blog/static/133546488201391832348289/和
http://hi.baidu.com/gsgaoshuang/item/17a8ed3c24d9b1ba134b14c2
先假如:数组的长度为10,数组元素为:25,19,6,58,34,10,7,98,160,0
整个希尔排序的算法过程如下如所示:

上图是原始数据和第一次选择的增量 d = 5。本次排序的结果如下图:

再举一例:
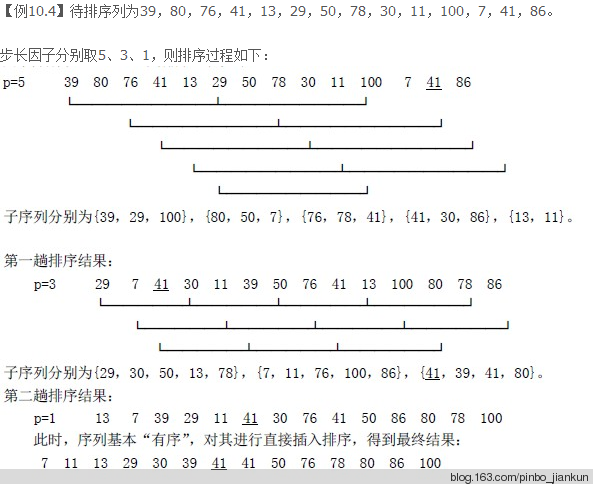
这个图下来 我估计大家都能看懂了。
接下来是源码时间: