extra1 二分查找与二叉判定树

一、二叉判定树

目录

• 一、二叉判定树
  • 1.二叉判定树
  • 2.长度为n的折半查找判定树的构造方法
  • 3.长度为10的折半查找判定树的具体生成过程
  • 4.补充：
  • 5.具体例子

1.二叉判定树

二叉判定树是用于描述解决问题的思路，比如可以使用判定树描述N个数的比较过程，是一种对过程的描述。
它也可以用于描述二分查找（即折半查找，以下都作二分查找）的过程。

描述二分查找的二叉判定树，我们也可以叫折半查找判定树，
从这样的判定树，我们可以分析二分查找算法的效率，

2.长度为n的折半查找判定树的构造方法

1. 当n=0时，折半查找判定树为空；
2. 当n＞0时，折半查找判定树的根结点是有序表中序号为mid=(n+1)/2的记录，根结点的左子树是与有序表r[1] ~ r[mid-1]相对应的折半查找判定树，根结点的右子树是与r[mid+1] ~ r[n]相对应的折半查找判定树。

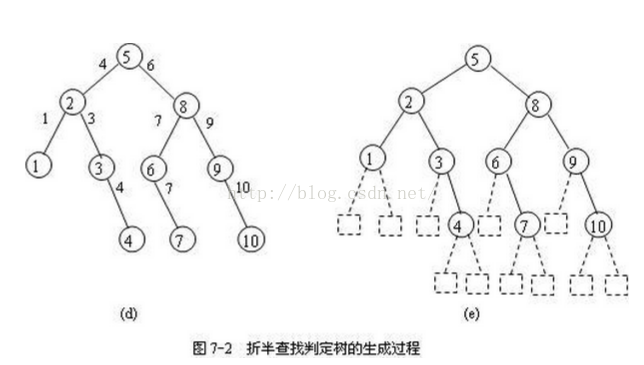
3.长度为10的折半查找判定树的具体生成过程

1. 在长度为10的有序表中进行折半查找，
   先和中间记录进行比较，而中间记录的序号为(1+10)/2=5，
   即判定树的根结点是5，如图7-2(a)所示；
2. 考虑判定树的左子树，即 将查找区间调整到左半区，此时的查找区间是[1，4]，也就是，左分支上根结点的值减1，代表查找区间的上限high，此时，根结点的左孩子是(1+4)/2=2，如图7-2(b)所示；
3. 考虑判定树的右子树，即 将查找区间调整到右半区，此时的查找区间是[6，10]，也就是，右分支上根结点的值加1，代表查找区间的下限low，此时，根结点的右孩子是(6+10)/2=8，如图7-2(c)所示；
4. 重复⑵⑶步，依次确定每个结点的左右孩子，不断缩小，如图7-2(d)所示。

4.补充：

1. 折半查找判定树 是一颗 二叉判定树 也是 一棵二叉排序/查找树，即每个结点的值均大于其左子树上所有结点的值，小于其右子树上所有结点的值；

2. 折半查找判定树中的结点都是查找成功的情况，
   而将每个结点的空指针指向的一个实际上并不存在的结点——称为外结点，所有外结点即是查找不成功的情况，
   如图7-2(e)虚线框所示。如果有序表的长度为n，则外结点一定有n+1个。

3. 在折半查找判定树中，某结点所在的层数即是查找该结点的比较次数。
   查找不成功时的比较次数即是查找相应外结点时与内结点的比较次数。

   或者换一种方式说：

   成功的折半查找过程，恰好是走了一条从根到被查记录的路径，比较次数恰为该记录在树中的层数。

   若查找失败，则其比较过程是一条根到某个外部结点的路径，比较次数是该路径上内部结点的总数。

4. 整个判定树代表的有序表的平均查找长度即为查找每个结点的比较次数之和除以有序表的长度。例如，长度为10的有序表的平均查找长度为： ASL=(1×1+2×2+3×4+4×3)/10=29/10
   整个判定树代表的有序表在查找失败时的平均查找长度即为查找每个外结点的比较次数之和除以外结点的个数（1+n）。例如，长度为10的有序表在查找失败时的平均查找长度为： ASL=(3×5+4×6)/11=39/11

   查找成功：

   ①（每层结点数 × 比较次数（层数））/n

   查找失败：
   ① 补全外节点
   ②（每层外节点数×比较次数（上一层层数））/（n+1）

5.具体例子

构造折半二叉树的流程
例：画出（3，17，22，27，40，55，61，75，80，91，97）的折半二叉树

①序列总长度为 n = 11 > 2^3 -1 = 7，即可判定二叉判定树为4层，第4层不满
②先画满n-1的完全二叉树
③还剩几个结点，遵循先右后左补全
④根据中序遍历顺序填入

结果如图：

查找流程：
比如查找75：
①查找成功，查找到第四层结点
②先拿75和55比较，75大，进入当前结点的左子树，反之进入右子树
③重复②，除非得到相等结果 或 找不到 以下一层的外节点表示。

​ 查找50：
​ ①查找失败，查找到第五层外节点
​ ②先拿50和55比较。55小，进入当前结点的右子树，反之进入左子树
​ ③重复②，除非得到相等结果 或 找不到 以下一层的外节点表示。

比较次数：
查找75：与55比较，与80比较，与61比较，与75比较得到结果——>4次
查找50：与55比较，与22比较，与27比较，与40比较得到外结点——>4次

查找成功时的平均查找长度：【查找每个结点的比较次数之和除以有序表的长度】
ASL=(1×1+2×2+3×4+4×4)/10=33/11=3

查找失败时的平均查找长度：【查找每个外结点的比较次数之和除以外结点的个数】
ASL=(3×4+4×8)/12=44/12=11/3