·~~~记两年前的一次数据结构大作业
一、题目选择
对课本上第二章的关于求多项式和的例题产生了比较浓厚的兴趣,并思考能否拓展对多项式的运算应用,于是又开辟出一些创新的运算,并尝试不同的算法(主要是对乘法运算,有的不太成功),最终确定了加法、减法、乘法、赋值求结果、求导、求不定积分、求定积分、插入单项等功能,并不断地简化步骤,使过程清晰易懂。
二、需求分析
主函数采取了switch-case选择结构,以实现对不同功能的切换选择,在它的外部辅助以do -while循环结构,每次循环结束前都输入一个数字字符以确定下一次循环需要选择验证的功能或者停止 程序。因此要求程序过程中能持续多次输入字符控制功能转换,不发生缓冲区溢出等程序停止工作的内存的问题。并且输入不同的字符,能准确地切换到与之对应的函数模块实现各自对应的功能。验收依据:验收者可以依次输入1-9,根据分别产生的提示进行不同的操作,通过自行运算与程序回显的结果进行比对,判断各自的功能是否准确完善。
三、概要设计
1.数据结构的设计
typedef struct pnode{ float coef; int exp; struct pnode *next; }polynode;
整体上使用了循环链表的数据结构(循环具体体现在Creat()函数内,稍后还有分析),定义的结构体包含了多项式系数coef(浮点型)、指数exp(整型)、链表指针域*next。多项式结构体名称定义为polynode。
多项式节点形式 : 系数 指数 指针
| coef | exp | * next |
例如 7+3x+9x3 +5x17可以表示为 :

2.设计方案论证
对于多项式相乘函数,我们曾探讨了两种方案:
对于两个多项式:
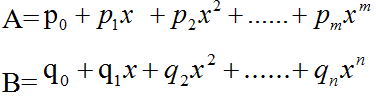
第一种就是作业源代码中的,这种思想是两个循环嵌套,先拿即A的第一项与B中的每个元素相乘,操作过程即两个指针的coef相乘且exp相加,保存在一个polynode类型的循环链表C里,再把C赋给另一个polynode类型的循环链表D里,把C置空。再拿即A的第二项与B的每一项分别相乘重新赋给C,与B每一项都乘完后把C和D相加(用到了多项式链表相加的函数polynode *Add(polynode *a,polynode *b),实现把b链表按升序加入到a链表里面,后面还有关于多项式相加函数的详解),然后再次置空C……以此类推,直到A的最后一项与B的每一项全乘完一遍得到的C再次加到D里面,得到的D即为A与B的乘积。函数返回D,然后打印出来。
第二种方案,与第一种前半部分基本一样,这种思想也是两个循环嵌套,先拿即A的第一项与B中的每个元素相乘,操作过程即两个指针的coef相乘且exp相加,保存在一个polynode类型的循环链表C里,再把C赋给另一个polynode类型的循环链表D里,把C置空。然后,A的第二项与B的第一项相乘,得到的结果作为单个节点插入D里面(这里需要一个函数polynode *Insert(polynode *a,polynode *b)旨在把单节点a插入到一个长链表b里面,然后返回新的b),接着与B的第二项、第三项……B的最后一项乘一遍,每乘一次马上插入D一次,然后A的第二项、第三项……A的最后一项都进行一次这个循环,最后函数返回D。(作业中使用的的乘法函数的是方法一,因为方法一运行更加快捷一些)。
3.函数模块描述
1 int Getvalue(polynode *head,int x)//多项式求值函数 2 { 3 int flag=0; 4 polynode *t=head->next; 5 while(t!=head) 6 { 7 flag+=t->coef*(pow(x,t->exp)); 8 t=t->next; 9 } 10 return flag; 11 }
主函数提供一个建立好的多项式链表head,并且给入一个X具体的值,实现把x带入链表对应的数学上的多项式得到一个结果,并返回这个结果。先把flag定义值为0,然后遍历head的每一项,当前flag等于上一次循环得到的flag值(或0)加上现在的幂值:t->coef乘以x的(t->exp)次方。
polynode *BDJF(polynode *head) //求不定积分函数 { polynode *p=head; p=p->next; while(p!=head) { p->coef=(p->coef)/(p->exp+1); p->exp+=1; p=p->next; } return head; }
上述函数是求不定积分,主函数会给一个已经创建完成的链表*head的头节点地址,操作时,定义个polynode类型p指针指向head第一个元素,进入循环,根据数学求积分的原理,先修改p此前指向的节点的系数为原来的(指数+1)倍,再修改指数,使指数值加一。然后p指针后移,再次判断现在的p是否指向head(因为是循环链表,所以不是NULL),如果不是,重复上述操作,直到head链表里面所有的节点的系数和指数都全部修改完毕返回head头指针。
float djf(polynode *head,float low,float high) //求定积分 { float d; head=BDJF(head); d=Getvalue(head,high)-Getvalue(head,low); return d; }
需要从主函数给出要求定积分的多项式链表以及上、下界具体浮点值。操作时,先利用BDJF(head)求出head的不定积分函数,接着再通过Getvalue(head,high)和Getvalue(head,low)求出上下界各自对应的值,做差,就是要求的多项式在某个区间上的值。
polynode *Differential(polynode *L) //求导函数 { polynode *p,*q,*pt; q=L; p=L->next; while(p!=L) { if(p->exp==0) { pt=p; p=p->next; q->next=p; free(pt); } else { p->coef=p->coef*p->exp; p->exp--; q=p; p=p->next; } } return(L); }
主函数提供一个多项式链表L,此函数实现对L的求导操作,即与前文的求不定积分操作恰恰相逆,p指针当前指向节点的系数coef等于p->coef*p->exp,然后修改指数exp,使其减一,修改完毕,p指向下一个节点:p=p->next。直到L全部遍历完成(p=L)循环结束。最后返回修改完的链表L头指针。其中有一步是用if判断指数exp是否为0,因为指数为零即纯系数项,求导值为0,为了节省空间,删除L里面这个部分,使用free()函数。
polynode *Insert(polynode *A,polynode *B) //实现在B链表 { //中按顺序插入单个结点A polynode *q1,*q2; q1=B; q2=B->next; while(q2&&A->exp>q2->exp) //查找插入位置 { q1=q2; q2=q2->next; } if(q2&&A->exp==q2->exp) //将指数相同项合并 { q2->exp+=A->exp; free(A); if(!q2->coef) //若系数相加和为0则释放节点 { q1->next=q2->next; free(q2); } } else //指数为新则插入新节点,改变前后连接逻辑 { A->next=q2; q1->next=A; } return B; }
此函数的目的其实有两个;其一,仅仅是在一个已经建立好的多项式链表B中插入一个单节点A,并返回现在的B,从而实现、检验链表的插入操作。其二,前面设计方案论证里提到的关于乘法函数的方法二说到,会使用一个插入函数,实现A中任一项与B中的任一项每乘一次都要把新节点插入到D里面,此函数可作为这种方法编写的乘法函数的重要的一部分。
polynode *Multiply(polynode *A,polynode *B) //实现两链表的乘法运算 { polynode * p,* q,* n,* temp,* m,*r; //定义当前指针p,q风别指向两链表和头指针,及新生成节点n int exp;//定义整型指数 float coef; r=(polynode *)malloc(sizeof(polynode));//为最后要得到的乘积链表*r开辟头节点 r->next=r; p=A->next;//当前指针跳过A链表头指向实际运算数 while(p!=A)//控制操作,循环A链表与内部while所控制B链表进行项之间的运算 { temp=(polynode *)malloc(sizeof(polynode));//在内部 创头节点为新生链表准备 即A中每一项与B中各项相乘构 成 一新链表 temp->next=NULL;//置空链表 m=temp;//临时变量,为后移指针做准备 q=B->next;//当前指针跳过B链表头指向实际运算数 while(q!=B) { n=(polynode *)malloc(sizeof(polynode)); //建立新节点 exp=p->exp+q->exp;//进行系数相加操作 coef=p->coef*q->coef; //进行指数相乘操作 n->coef=coef;//赋值新节点的系数域 n->exp=exp; //赋值新节点的指数域 m->next=n; //链接节点至头结点,构成链表 m=m->next;//后移指针,为下一节点做准备 q=q->next;//控制B链表下一项 } p=p->next; //控制A链表下一项 m->next=temp; Add(r,temp); } return r;
}
乘法运算的思想在前面的“设计论证模块”里已经详细的说明了,这里就在此解释(其中,由于乘法的复杂性、核心性,为了方便理解,我在上面的代码后加入了必要的注释)。
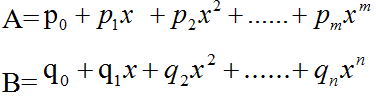
这种思想是两个循环嵌套,先拿p0(即A的第一项)与B中的每个元素相乘,操作过程即两个指针的coef相乘且exp相加,保存在一个polynode类型的循环链表temp里,再把temp加到另一个polynode类型的循环链表r(r一开始为空循环链表)里,把temp置空。再拿p1x即A的第二项与B的每一项分别相乘重新赋给temp,与B每一项都乘完后再把temp和r相加(用到了多项式链表相加的函数polynode *Add(polynode *a,polynode *b),实现把b链表按升序加入到a链表里面),然后再次置空temp......以此类推,直到A的最后一项pmxm与B的每一项全乘完一遍得到的temp再次加到r里面,得到的r即为A与B的乘积。函数返回r,然后在主函数里面打来。
四、详细设计
这里我开始介绍主函数的构造。

以上是主函数前一部分,作用就是功能执行前的声明与定义。这里便不逐个介绍,后面还会提到。

接下来是循环-选择部分,也是主函数的核心。首先输入字符‘ch’,为进入循环的switch(ch)部分做选择做准备,以确定切换的不同的功能。而循环使用的是
do
{
.....
}while 的循环结构。循环里面是一个完整的switch—case‘...’选择结构 ,意图实现选择功能,case里面就是字符‘ch’对应的不同的功能。

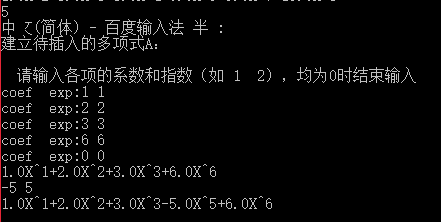
Ch=‘1’时,先逐次建立两个多项式链表,第一个是ha,第二个是hb,建立完后立刻输出(Output函数)刚刚建立的多项式,以确定是否正确。然后执行Add(ha,hb)加法函数,结果返回给ha,并输出。

Ch=‘2’时,先逐次建立两个多项式链表,第一个是ha,第二个是hb,建立完后立刻输出(Output函数)刚刚建立的多项式,以确定是否正确。然后执行Del(ha,hb)减法函数,结果返回给ha,并输出。

Ch=‘3’时,只需要建立一个多项式链表ha并输出,接着输出(Output())把ha求导(Differential(ha))得到的多项式。

Ch=‘4’时,先逐次建立两个多项式链表,第一个是ha,第二个是hb,建立完后立刻输出(Output函数)刚刚建立的多项式,以确定是否正确。然后执行Multiply(ha,hb)乘法函数,结果返回给hc,并输出hc。

Ch=‘5’时,先建立ha并输出,然后建立要插入ha里面的单节点hc,对它的系数、指数赋值,通过函数Insert(hc,ha)实现按幂值递增顺序插入ha并且返回值赋给ha,然后打印。

Ch=‘6’时,先建立ha并输出,然后输入用于计算的底数,赋给x,通过Getvalue(ha,x)返回求得的数值,在printf()函数里面直接打印出来。

` Ch=‘7’时,先建立ha并输出,然后带入BDJF(ha)求ha的不定积分并且赋给hb,并输出。

Ch=‘8’时,先建立ha并输出,然后输入定积分的下界m和上界n,代入djf(ha,m,n)求出定积分,包含在printf()里面输出。
当输入ch=‘9’时结束程序。Switch-case选择结束之后,为了给下一次循环作出判断,需要再输入ch字符,而循环是否继续的条件就是判断本次输入的ch是否等于‘9’。
五、测试结果
界面
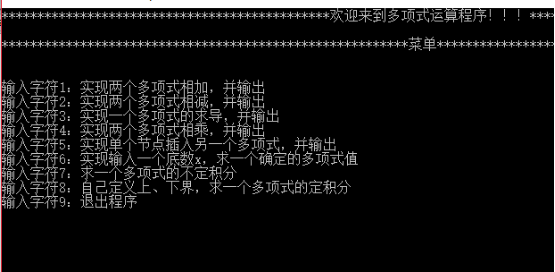
加法
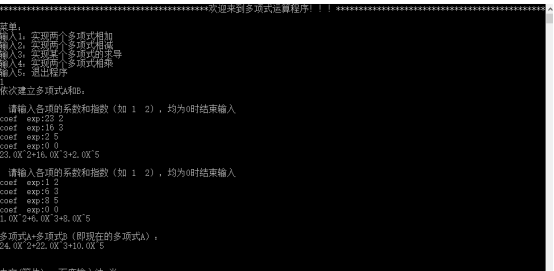

减法


乘法
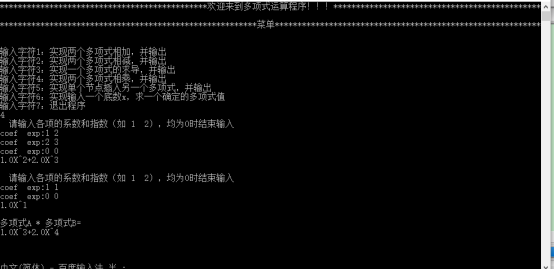

求导

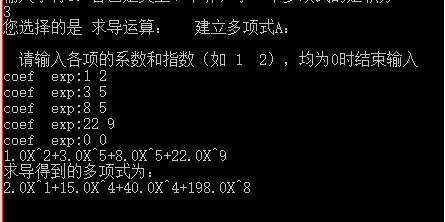
插入一项

求具体值


求不定积分


求定积分


六、程序流程图
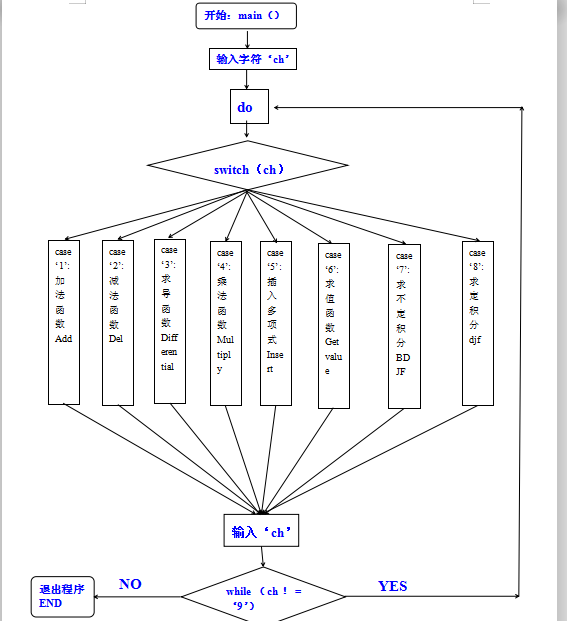
七、源代码
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<conio.h> 4 #include<malloc.h> 5 #include<math.h> 6 typedef struct pnode //数据结构 7 { 8 float coef; //系数项 9 int exp; //指数项 10 struct pnode *next; 11 }polynode; 12 polynode *Creat() //创建多项式 13 { 14 float coef; 15 int exp; 16 polynode *head,*s,*r; 17 head=(polynode*)malloc(sizeof(polynode)); 18 head->coef=0; //初始化 19 head->exp=-1; 20 r=head; 21 printf(" 请输入各项的系数和指数(如 1 2),均为0时结束输入 "); 22 while(1) 23 { 24 printf("coef exp:"); 25 scanf("%f %d",&coef,&exp); 26 if(coef!=0) 27 { 28 s=(polynode*)malloc(sizeof(polynode)); 29 s->coef=coef; 30 s->exp=exp; 31 r->next=s; 32 r=s; 33 } 34 else break; 35 } 36 r->next=head; //循环链表 首尾相连 37 return head; 38 } 39 polynode *Add(polynode *pa,polynode *pb) //多项式相加运算函数 40 { 41 polynode *p,*q,*r,*s; 42 float x; 43 p=pa->next; 44 q=pb->next; 45 s=pa; 46 while((p!=pa)&&(q!=pb)) 47 { 48 if(p->exp<q->exp) 49 { 50 s=p; 51 p=p->next; 52 } 53 if(p->exp>q->exp) 54 { 55 r=q->next; 56 q->next=p; 57 s->next=q; 58 s=q; 59 q=r; 60 } 61 else 62 { 63 x=p->coef+q->coef; 64 if(x!=0) 65 { 66 p->coef=x; 67 s=p; 68 } 69 else 70 { 71 s->next=p->next; 72 free(p); 73 } 74 p=s->next; 75 r=q; 76 q=q->next; 77 free(r); 78 } 79 } 80 if(q!=pb) 81 { 82 r=q; 83 while(r->next!=pb) 84 r=r->next; 85 s->next=q; 86 r->next=pa; 87 } 88 return pa; 89 } 90 polynode *Del(polynode *pa,polynode *pb) //多项式减法运算函数 91 { 92 polynode *p,*q,*r,*s; 93 float x; 94 p=pa->next; 95 q=pb->next; 96 s=pa; 97 while((p!=pa)&&(q!=pb)) 98 { 99 if(p->exp<q->exp) 100 { 101 s=p; 102 p=p->next; 103 } 104 if(p->exp>q->exp) 105 { 106 q->coef=-(q->coef); 107 r=q->next; 108 q->next=p; 109 s->next=q; 110 s=q; 111 q=r; 112 } 113 else 114 { 115 x=p->coef-q->coef; 116 if(x!=0) 117 { 118 p->coef=x; 119 s=p; 120 } 121 else 122 { 123 s->next=p->next; 124 free(p); 125 } 126 p=s->next; 127 r=q; 128 q=q->next; 129 free(r); 130 } 131 } 132 if(q!=pb) 133 { 134 r=q; 135 q->coef=-(q->coef); 136 while(r->next!=pb) 137 { 138 r=r->next; 139 r->coef=-(r->coef); 140 } 141 s->next=q; 142 r->next=pa; 143 } 144 return pa; 145 } 146 polynode *BDJF(polynode *head) //求不定积分函数 147 { 148 polynode *p=head; 149 p=p->next; 150 while(p!=head) 151 { 152 p->coef=(p->coef)/(p->exp+1); 153 p->exp+=1; 154 p=p->next; 155 } 156 return head; 157 } 158 int djf(polynode *head,int low,int high) //求定积分函数 159 { 160 int d; 161 head=BDJF(head); 162 d=Getvalue(head,high)-Getvalue(head,low); 163 return d; 164 } 165 polynode *Multiply(polynode *A,polynode *B) //实现两链表的乘法运算 166 { 167 polynode * p,* q,* n,* temp,* m,*r; //定义当前指针p,q风别指向两链表和头指针,尾指针,及新生成节点n 168 int exp; //定义整型指数 169 float coef; 170 r=(polynode *)malloc(sizeof(polynode)); //为最后要得到的乘积链表*r开辟头节点 171 r->next=r; //体现循环链表的操作 172 p=A->next; //当前指针跳过A链表头指向实际运算数 173 while(p!=A) //控制操作,循环A链表与内部while所控制B链表进行项之间的运算 174 { 175 temp=(polynode *)malloc(sizeof(polynode)); //在内部创头节点为新生链表准备 即A中每一项与B中各项相乘构成一新链表 176 temp->next=NULL; //置空链表 177 m=temp; //临时变量,为后移指针做准备 178 q=B->next; //当前指针跳过B链表头指向实际运算数 179 while(q!=B) 180 { 181 n=(polynode *)malloc(sizeof(polynode)); //建立新节点 182 exp=p->exp+q->exp; //进行系数相加操作 183 coef=p->coef*q->coef; // //进行指数相乘操作 184 n->coef=coef; //赋值新节点的系数域 185 n->exp=exp; //赋值新节点的指数域 186 m->next=n; //链接节点至头结点,构成链表 187 m=m->next; //后移指针,为下一节点做准备 188 q=q->next; //控制B链表下一项 189 } 190 p=p->next; //控制A链表下一项 191 m->next=temp; 192 Add(r,temp); 193 } 194 return r; 195 } 196 int Getvalue(polynode *head,int x) //求多项式值的函数 197 { 198 int flag=0; 199 polynode *t=head->next; 200 while(t!=head) 201 { 202 flag+=t->coef*(pow(x,t->exp)); 203 t=t->next; 204 } 205 return flag; 206 } 207 void Output(polynode *head) //输出多项式 208 { 209 polynode *p; 210 p=head->next; 211 printf("%.1fX^%d",p->coef,p->exp); 212 while(p!=head) 213 { 214 p=p->next; 215 if(p!=head) 216 if(p->coef>0) printf("+%.1fX^%d",p->coef,p->exp); //输出各项的稀疏和指数 217 else printf("%.1fX^%d",p->coef,p->exp); 218 else break; 219 } 220 printf(" "); 221 } 222 polynode *Differential(polynode *L) //求导函数 223 { 224 polynode *p,*q,*pt; 225 q=L; 226 p=L->next; 227 while(p!=L) 228 { 229 if(p->exp==0) 230 { 231 pt=p; 232 p=p->next; 233 q->next=p; 234 free(pt); 235 } 236 else 237 { 238 p->coef=p->coef*p->exp; 239 p->exp--; 240 q=p; 241 p=p->next; 242 } 243 } 244 return L; 245 } 246 polynode *Insert(polynode *A,polynode *B) //实现在B链表中按顺序插入单个结点A 247 { 248 polynode *q1,*q2; 249 q1=B; 250 q2=B->next; 251 while(q2&&A->exp>q2->exp) //查找插入位置 252 { 253 q1=q2; 254 q2=q2->next; 255 } 256 if(q2&&A->exp==q2->exp) //将指数相同项合并 257 { 258 q2->exp+=A->exp; 259 free(A); 260 if(!q2->coef) //若系数相加和为0则释放节点 261 { 262 q1->next=q2->next; 263 free(q2); 264 } 265 } 266 else //指数为新则插入新节点,改变前后连接逻辑 267 { 268 A->next=q2; 269 q1->next=A; 270 } 271 return B; 272 } 273 int main() 274 { 275 char ch; 276 int x; 277 int m,n; 278 polynode *ha,*hb,*hc; 279 printf("**********************************************欢迎来到多项式运算程序!!!********************************************** "); 280 printf("*********************************************************菜单*********************************************************** "); 281 printf(" 输入字符1:实现两个多项式相加,并输出"); 282 printf(" 输入字符2:实现两个多项式相减,并输出"); 283 printf(" 输入字符3:实现一个多项式的求导,并输出"); 284 printf(" 输入字符4:实现两个多项式相乘,并输出"); 285 printf(" 输入字符5:实现单个节点插入另一个多项式,并输出"); 286 printf(" 输入字符6:实现输入一个底数x,求一个确定的多项式值"); 287 printf(" 输入字符7:求一个多项式的不定积分"); 288 printf(" 输入字符8:自己定义上、下界,求一个多项式的定积分 "); 289 ch=getche(); 290 do 291 { 292 switch(ch) //选择开关,循环使用,键‘9’结束程序 293 { 294 case '1': 295 printf(" 您选择的是 加法运算: 依次建立多项式A和B: "); 296 ha=Creat(); 297 Output(ha); 298 hb=Creat(); 299 Output(hb); 300 ha=Add(ha,hb); 301 printf("多项式A+多项式B(即现在的多项式A): "); 302 Output(ha); 303 break; 304 case '2': 305 printf(" 您选择的是 减法运算: 依次建立多项式A和B: "); 306 ha=Creat(); 307 Output(ha); 308 hb=Creat(); 309 Output(hb); 310 ha=Del(ha,hb); 311 printf("多项式A-多项式B(即现在的多项式A): "); 312 Output(ha); 313 break; 314 case '3': 315 printf(" 您选择的是 求导运算: 建立多项式A: "); 316 ha=Creat(); 317 Output(ha); 318 printf("求导得到的多项式为: "); 319 Output(Differential(ha)); 320 break; 321 case '4': 322 printf(" 您选择的是 乘法运算: 依次建立多项式A和B: "); 323 ha=Creat(); 324 Output(ha); 325 hb=Creat(); 326 Output(hb); 327 hc=Multiply(ha,hb); 328 printf(" 多项式A * 多项式B= "); 329 Output(hc); 330 break; 331 case '5': 332 printf(" 建立待插入的多项式A: "); 333 ha=Creat(); 334 Output(ha); 335 hc=(polynode*)malloc(sizeof(polynode)); 336 scanf("%f %d",&hc->coef,&hc->exp); 337 ha=Insert(hc,ha); 338 printf("插入以后的多项式为:"); 339 Output(ha); 340 break; 341 case '6': 342 printf(" 您选择的是赋值计算 建立多项式ha: "); 343 ha=Creat(); 344 Output(ha); 345 printf("请确定底数x的值(要求x是自然数): "); 346 scanf("%d",&x); 347 printf(" 把x=%d带入ha多项式中得到其值为:%d ",x,Getvalue(ha,x)); 348 break; 349 case '7': 350 printf(" 您选择的是 求不定积分运算: 建立多项式A: "); 351 ha=Creat(); 352 Output(ha); 353 printf("取得的不定积分是: "); 354 hb=BDJF(ha); 355 Output(hb); 356 break; 357 case '8': 358 printf(" 您选择的是 求定积分运算: 建立多项式A: "); 359 ha=Creat(); 360 Output(ha); 361 printf("分别输入下界m和上界n: "); 362 scanf("%d%d",&m,&n); 363 printf("取得的定积分是: %d ",djf(ha,m,n)); 364 break; 365 default: printf("请输入有效字符! "); 366 } 367 ch=getche(); 368 printf(" "); 369 } 370 while(ch!='9'); 371 return 0; 372 }