二叉树相关概念

一. 二叉树基本概念

在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。二叉树是每个结点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

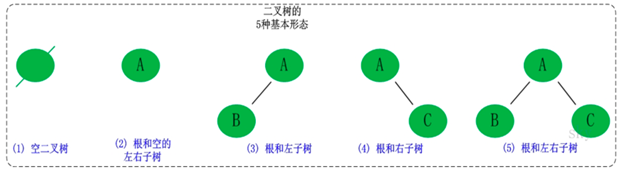
1. 二叉树的分类

• (1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。或者说只有最下面两层结点的度可以小于2，并且最下层的 叶结点几种在靠左的若干位置上。
• (2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
• (3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
• (4)

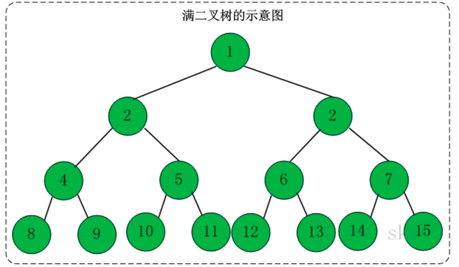
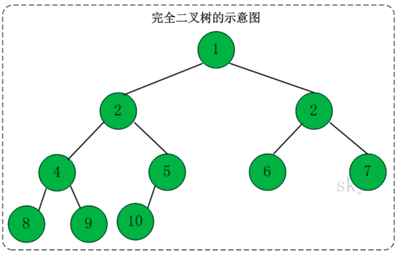
举例：

面试题：如果一个完全二叉树的结点总数为768个，求叶子结点的个数。
由二叉树的性质知：n0=n2+1，将之带入768=n0+n1+n2中得：768=n1+2n2+1，因为完全二叉树度为1的结点个数要么为0，要么为1，那么就把n1=0或者1都代入公式中，很容易发现n1=1才符合条件。所以算出来n2=383，所以叶子结点个数n0=n2+1=384。

总结规律：如果一棵完全二叉树的结点总数为n，那么叶子结点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）

2. 二叉树的性质

性质1：二叉树第i层上的结点数目最多为2^i-1(i>=1)

性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）

性质3：包含n个结点的二叉树的高度至少为(log₂n)+1

性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

3. 二叉树的用途

（1）可以用作二叉查找树（也叫二叉搜索树）：设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]

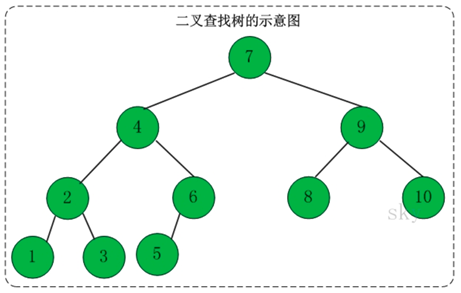
note:在二叉查找树中有以下性质：

• （1）若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
• （2）任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
• （3）任意结点的左、右子树也分别为二叉查找树。
• （4）没有键值相等的结点。

二. 相关术语

结点的度：结点拥有的子树的数目. 与图论中的“度”不同，树的度是如下定义的：有根树T中，结点x的子女数目称为x的度。也就是：在树中，结点有几个分叉，度就是几

                   一个有用的小公式：树中结点数 = 总分叉数 +1。(这里的分叉数就是所有结点的度之和)

叶子结点：度为0的结点

分支结点：度不为0的结点

树的度：树中结点的最大的度

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1-----(同深度)

树的高度：树中结点的最大层次。从下往上数，最下面是高度为1

树的深度：从上往下数，最上面根部分是深度为1

森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

举例：

设树T的度为4，其中度为1，2，3，4的节点个数分别为4，2，1，1，则T中的叶子数为？

解答：
叶子的度数为0；那么设叶子数为x，则此树的总分叉数为1*4+2*2+3*1+4*1=15；此树的节点个数为16（此处涉及到一个公式;节点数=分叉数+1，由图形便可以观察出来）。又根据题目可以知道顶点数目还可以列出一个式子：4+2+1+1+x便可以得到等式：4+2+1+1+x=16；x=8为叶子数。
因为此题是数据结构中的问题：一般情况下都是有向树，所以叶子节点的度数为0，要区分于离散数学中的无向树叶子节点度为一。在数据结构中一般常用的公式为：二叉树：度为0的节点数=度为2的节点数+1（n0=n2+1）此公式可由上述计算思想推导（一般在二叉树那里的公式多一些，树中只要你明确定义，画出图来，便可以根据图形寻找出规律来）

三. 二叉树的遍历方式

• 先序遍历：遍历顺序规则为【根左右】(DFS思想)
• 中序遍历：遍历顺序规则为【左根右】(DFS思想)
• 后序遍历：遍历顺序规则为【左右根】(DFS思想)
• 层次遍历：实际上用的是广度优先算法BFS(Breadth-First Search)

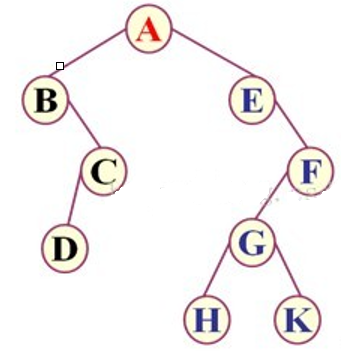
比如：上面的二叉树三种方式遍历后的情况是：

先序遍历：ABCDEFGHK

中序遍历：BDCAEHGKF

后序遍历：DCBHKGFEA

 前三种遍历方式的递归代码：

//后序遍历，左=》右=》根
    public void postorder_Traversal(TreeNode root)
    {
        if(root==null)return;
        postorder_Traversal(root.left);
        postorder_Traversal(root.right);
        
         //访问节点的逻辑代码块
        System.out.print(root.val+" ");
    }
    //前序遍历，根=》左=》右
    public void preorder_Traversal(TreeNode root)
    {
        if(root==null)return;
        
        //访问节点的逻辑代码块
        System.out.print(root.val+" ");
        
        preorder_Traversal(root.left);
        preorder_Traversal(root.right);
    }
    //中序遍历，左=》根=》右
    public void inorder_Traversal(TreeNode root)
    {
        if(root==null)return;
        inorder_Traversal(root.left);
        
         //访问节点的逻辑代码块
        System.out.print(root.val+" ");
        
        inorder_Traversal(root.right);
    }

层次遍历思想：

根据层次遍历的顺序，每一层都是从左到右的遍历输出，借助于一个队列。

先将根节点入队，当前节点是队头节点，将其出队并访问，如果当前节点的左节点不为空将左节点入队，如果当前节点的右节点不为空将其入队。所以出队顺序也是从左到右依次出队。

import java.util.LinkedList;
 
public class LevelOrder
{
  public void levelIterator(BiTree root)
  {
      if(root == null)
      {
          return ;
      }
      LinkedList<BiTree> queue = new LinkedList<BiTree>();
      BiTree current = null;
      queue.offer(root);//将根节点入队
      while(!queue.isEmpty())
      {
          current = queue.poll();//出队队头元素并访问
          System.out.print(current.val +"-->");
          if(current.left != null)//如果当前节点的左节点不为空入队
          {
              queue.offer(current.left);
          }
          if(current.right != null)//如果当前节点的右节点不为空，把右节点入队
          {
              queue.offer(current.right);
          }
      }
      
  }
 
}

note:上面的root应该代表了整棵树

或者：

public static void levelRead(TreeNode root)
{
    if(root == null) return;
    Queue<TreeNode> queue = new LinkedList<TreeNode>() ;
    queue.add(root);
    while(queue.size() != 0)
    {
        int len = queue.size();
        for(int i=0;i <len; i++)
        {
            TreeNode temp = queue.poll();
            System.out.print(temp.val+" ");
            if(temp.left != null)  queue.add(temp.left);
            if(temp.right != null) queue.add(temp.right);
        }
    }
}

note:poll是取出并且移除队列的头结点；peek是取出但是并不移除队列的头节点；offer将元素加入到队列的末尾；

四. 二叉树的建立