来源:力扣(LeetCode)- 面试题10.1
问题
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
解题
斐波那契数列的定义是 f(n+1)=f(n)+f(n−1) ,生成第 n 项的做法有以下几种:
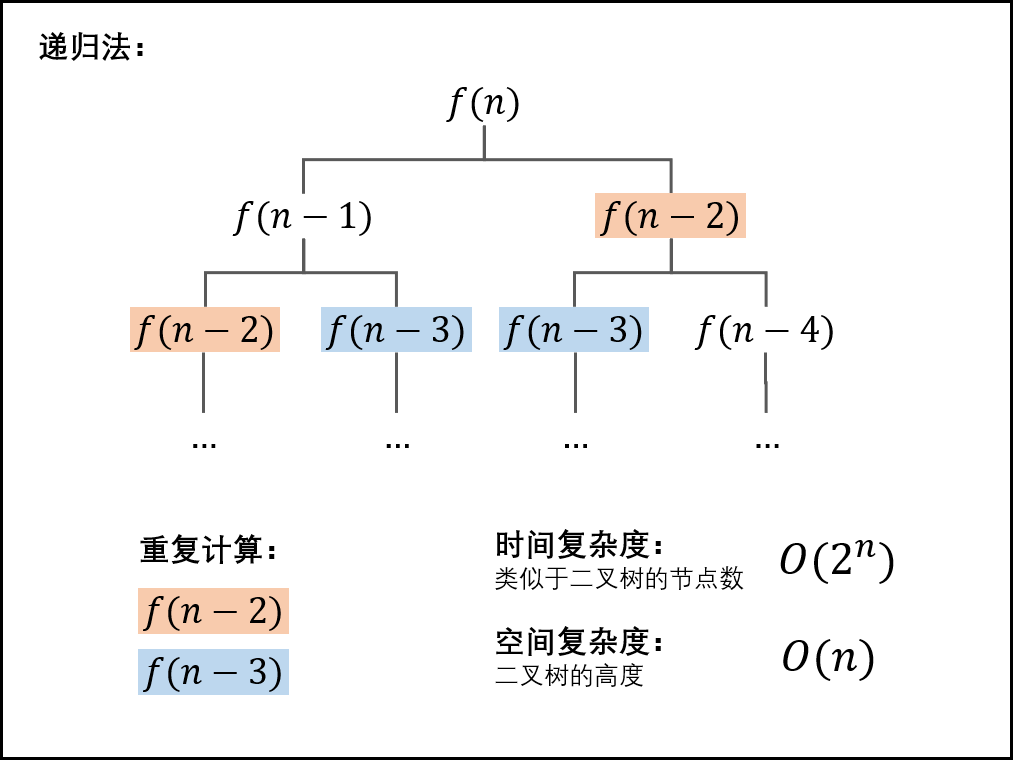
递归法
- 原理: 把 f(n) 问题的计算拆分成 f(n−1) 和 f(n−2) 两个子问题的计算,并递归,以f(0) 和 f(1) 为终止条件。
- 缺点: 大量重复的递归计算,例如 f(n) 和 f(n−1) 两者向下递归需要 各自计算 f(n−2) 的值。
记忆化递归法
- 原理: 在递归法的基础上,新建一个长度为 n 的数组,用于在递归时存储 f(0) 至 f(n) 的数字值,重复遇到某数字则直接从数组取用,避免了重复的递归计算。
- 缺点: 记忆化存储需要使用 O(N) 的额外空间。
动态规划
- 原理: 以斐波那契数列性质 f(n+1)=f(n)+f(n−1) 为转移方程。
- 从计算效率、空间复杂度上看,动态规划是本题的最佳解法。
动态规划解析
- 状态定义: 设 dp 为一维数组,其中 dp[i] 的值代表斐波那契数列第 i 个数字 。
- 转移方程:dp[i+1]=dp[i]+dp[i−1] ,即对应数列定义 f(n+1)=f(n)+f(n−1) 。
- 初始状态: dp[0] = 0, dp[1] = 1 ,即初始化前两个数字。
- 返回值: dp[n] ,即斐波那契数列的第 n 个数字。
空间复杂度优化
若新建长度为 n 的 dp 列表,则空间复杂度为O(N)。
- 由于 dp 列表第 i 项只与第 i−1 和第 i−2 项有关,因此只需要初始化三个整形变量 sum, a, b ,利用辅助变量 sum 使 a,b 两数字交替前进即可。
- 节省了 dp 列表空间,因此空间复杂度降至 O(1) 。
循环求余法
大数越界:随着 n 增大, f(n) 会超过 Int32 甚至 Int64 的取值范围,导致最终的返回值错误。
- 求余运算规则: 设正整数 x, y, p,求余符号为 ⊙ ,则有 (x + y) ⊙ p = (x ⊙ p + y ⊙ p) ⊙ p 。
- 解析: 根据以上规则,可推出 f(n)⊙p=[f(n−1)⊙p+f(n−2)⊙p]⊙p ,从而可以在循环过程中每次计算 sum = (a + b) ⊙ 1000000007 ,此操作与最终返回前取余等价。

复杂度分析
- 时间复杂度 O(N) : 计算 f(n) 需循环 n 次,每轮循环内计算操作使用 O(1) 。
- 空间复杂度 O(1) : 几个标志变量使用常数大小的额外空间。
代码
class Solution {
public int fib(int n) {
int a = 0, b = 1, sum;
for(int i = 0; i < n; i++){
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
}