点分治
关于点分治,其实思想是非常好理解的,类比在数列上或是在平面上的分治算法(如归并排序,平面最近点对等),我们可以从字面上理解该算法:
以一个点为界限,将一棵树分成若干个子树,当划分到一定规模,就对每个子树分别进行求解
感性理解就好了
感受一个算法最直观的办法,就是来看一道模板题。
【模板】 点分治
给定一棵有(n)个点的树,询问树上长度为(k)的链是否存在。
首先可以很直观的知道,对于树上的任意一个点,有很多条经过它的链
那么,对于本题,我们是否可以在能够接受的时间内对这些经过该点的链进行求解呢?
答案是肯定的,只需要以该节点为根节点,对整颗树进行一遍( ext{DFS}),求出各个点到该点的距离,然后就可以用桶排等方法解决该问题。
那么对于剩下的没有被处理到的链呢?
自然,我们可以以这个点,将整棵树断掉,将它的子树分开递归分治求解,这样这道题目就解决啦!
咳咳,真的这么简单吗?
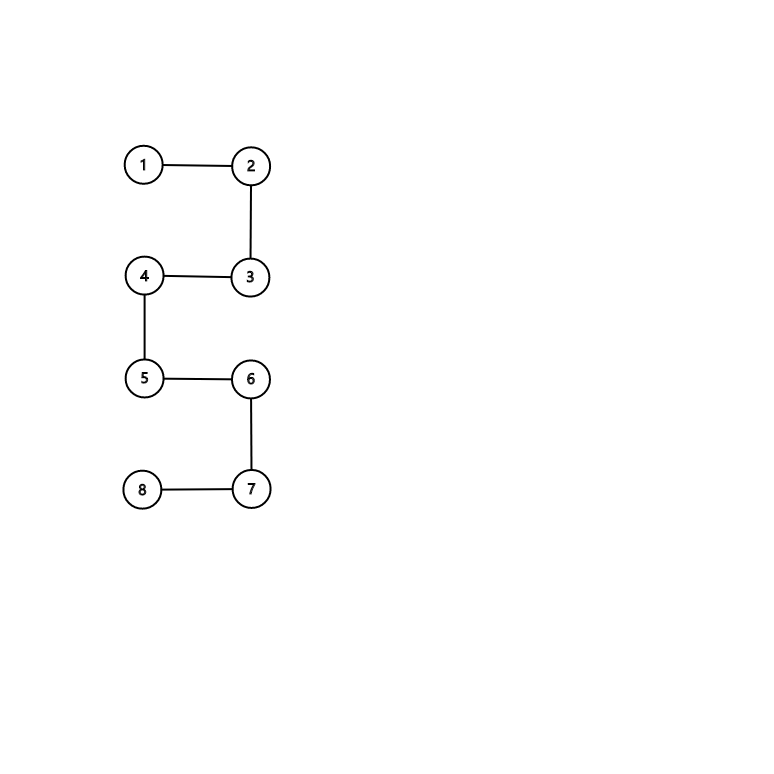
我们来看一张图
多么优雅的一条链!
如果我们一开始以(1)为根节点,按照这个思路,我们需要进行(n)次操作,这样肯定是不行的。
也就是说,我们需要找到一个节点,使得在将其断掉之后,剩下的各个子树的大小相对均匀,这样在进行分治求解的时候就可以让时间复杂度最优。
所以这里需要引入一个新的概念:
树的重心
定义:树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵子树尽可能平衡。(摘自百度百科)
那么如何求树的重心呢?
我们可以采取一种类似于(DP)的算法,因为我们要使最大的子树节点数最少,于是我们可以任选一个点进行(DFS),在搜索过程中,记录每一个点的最大的子树大小,然后进行操作,即
(sum)表示这颗子树一共有多少个节点,(siz[i])即子树大小
这样的话,我们就只需要在该子树中找到最小的(dp[i]),这样(i)就是我们要找的重心了。
是不是很简单?
贴一小段代码
//root默认为0,dp[0]=inf
void get_root(int u,int fa,int sum)
{
dp[u]=0,siz[u]=1;//初始化
for(int i=head[u];i;i=e[i].nex)
{
int v=e[i].to;
if(v==fa||vis[u]) continue;//vis[u]表示该节点是否被当作根节点操作过,同时保证该函数只在本子树内操作
get_root(v,u,sum);
siz[u]+=siz[v];
dp[u]=max(dp[u],siz[v]);
}
dp[u]=max(dp[u],sum-siz[u]);
if(dp[u]<dp[root]) root=u;
}
那么,如何统计答案呢?
对于本题,提供(3)种方法供君选择
说明:(dis[u])表示(u)节点到重心的距离,(siz[u])表示以(u)为根的子树大小,(root)表示当前子树重心
(1.)暴力枚举法
我们将所有的节点到重心的距离(dis[u])通过一遍(DFS)记录下来,然后开一个桶,两两组合,统计答案。这样的话,会有一个问题,就是在同一条路径上的节点的答案也会被统计,比如(dis[u]+dis[son[u]]=k),但是这两个节点并没有到重心的一条链,所以需要删去。
那么如何做呢?
简单容斥一下就好了
时间复杂度为单次(O(siz[root]^2)),且有一定局限性——(k)太大时无法使用
$ 2.$配对法
这是一个在本题跑得飞起的计算方法
假设一共有(son_1,son_2,son_3,...,son_n)这些多棵子树
令(vis[j])数组表示在求解到第(i)棵子树的答案时,前(i-1)棵子树是否存在到重心长度为(j)的路径
这样一来,我们就只需要在每棵子树当中对于每一个询问,枚举找到可以凑成答案的路径即可
时间复杂度为单次(O(m*siz[root])),由于询问较少,跑的飞起
但注意,在还原数组的时候,需要将
同样,也有一定的局限性——(k)太大时同样无法使用
(3.)two pointers
维护(l,r)两个指针,将所有得到的(dis[i])从小到大排序,这样的话,就可以保证(dis)数组单调递增,有两个思路供君选择:
(1))直接标记(仅针对本题)
在(DFS)求解(dis[i])时,可以记录每一个节点对应来自哪一棵子树,记为(tag[i])然后可以按照这样的思路:
令(l=0,r=siz[root])
如果当前点已有答案,跳过
如果(dis[l]+dis[r]>k),就(--r),这样才有可能有解
如果(dis[l]+dis[r]<k),就(++l),同理
如果(dis[l]+dis[r]=k quad且quad tag[l]==tag[r]),就看(dis[r-1])的大小,并进行相应调整
如果上述条件都不满足,则对于这个(k)有解
(2))前缀统计
我们可以化等为不等,记录(le k)和(le k-1)的路径条数
同样令(l=0,r=siz[root])
若(dis[l]+dis[r]<=k),则说明在([l+1,r])的(dis)都可以组成答案,此时(++l);
否则(--r);
这种方法同样需要容斥。
两种方法的时间复杂度均为单次(O(m*siz[root])),且不受(k)的限制,同时这种思想也在非常多的题目上有所运用,如(NOI2019Day1T3)
大体思路就是这样,共(3)步:
(1.)找树的重心
(2.)求解经过重心的链对答案的贡献
(3.)在各个子树内求解
于是这个题目就完结辣OWO~
贴代码(上面讲的很清楚了于是没有注释QWQ)
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m;
struct cc{
int to,nex,w;
}e[maxn<<2];
int head[maxn],cnt;
int siz[maxn],dp[maxn],vis[maxn],q[maxn],ans[maxn];
void add(int x,int y,int z)
{
++cnt;
e[cnt].to=y;
e[cnt].nex=head[x];
e[cnt].w=z;
head[x]=cnt;
}
int root=0;
void get_root(int u,int fa,int sum)
{
dp[u]=0,siz[u]=1;
for(int i=head[u];i;i=e[i].nex)
{
int v=e[i].to;
if(v==fa||vis[v]) continue;
get_root(v,u,sum);
siz[u]+=siz[v];
dp[u]=max(dp[u],siz[v]);
}
dp[u]=max(dp[u],sum-siz[u]);
if(dp[u]<dp[root]) root=u;
}
int dep[maxn],dis[maxn],tot;
void get_dis(int u,int fa)
{
dep[++tot]=dis[u];
for(int i=head[u];i;i=e[i].nex)
{
int v=e[i].to;
if(v==fa||vis[v]) continue;
dis[v]=dis[u]+e[i].w,get_dis(v,u);
}
}
void get_ans(int u,int now,int val)
{
dis[u]=now,tot=0;
get_dis(u,0);
stable_sort(dep+1,dep+tot+1);
for(int i=1;i<=m;++i)
{
int s1=0,s2=0,l=1,r=tot;
while(l<r)
if(dep[l]+dep[r]<=q[i]) s1+=r-l,++l;
else --r;
l=1,r=tot;
while(l<r)
if(dep[l]+dep[r]<q[i]) s2+=r-l,++l;
else --r;
ans[i]+=(s1-s2)*val;
}
}
void solve(int u)
{
get_ans(u,0,1);
vis[u]=1;
for(int i=head[u];i;i=e[i].nex)
{
int v=e[i].to;
if(vis[v]) continue;
get_ans(v,e[i].w,-1);
root=0;
get_root(v,u,siz[v]),solve(root);
}
}
int main()
{
int a,b,c;
scanf("%d%d",&n,&m);
dp[0]=n;
for(int i=1;i<n;++i)
scanf("%d%d%d",&a,&b,&c),add(a,b,c),add(b,a,c);
for(int i=1;i<=m;++i) scanf("%d",&q[i]);
get_root(1,0,n);solve(root);
for(int i=1;i<=m;++i)
printf("%s
",ans[i]?"AYE":"NAY");
return 0;
}