题目如图:
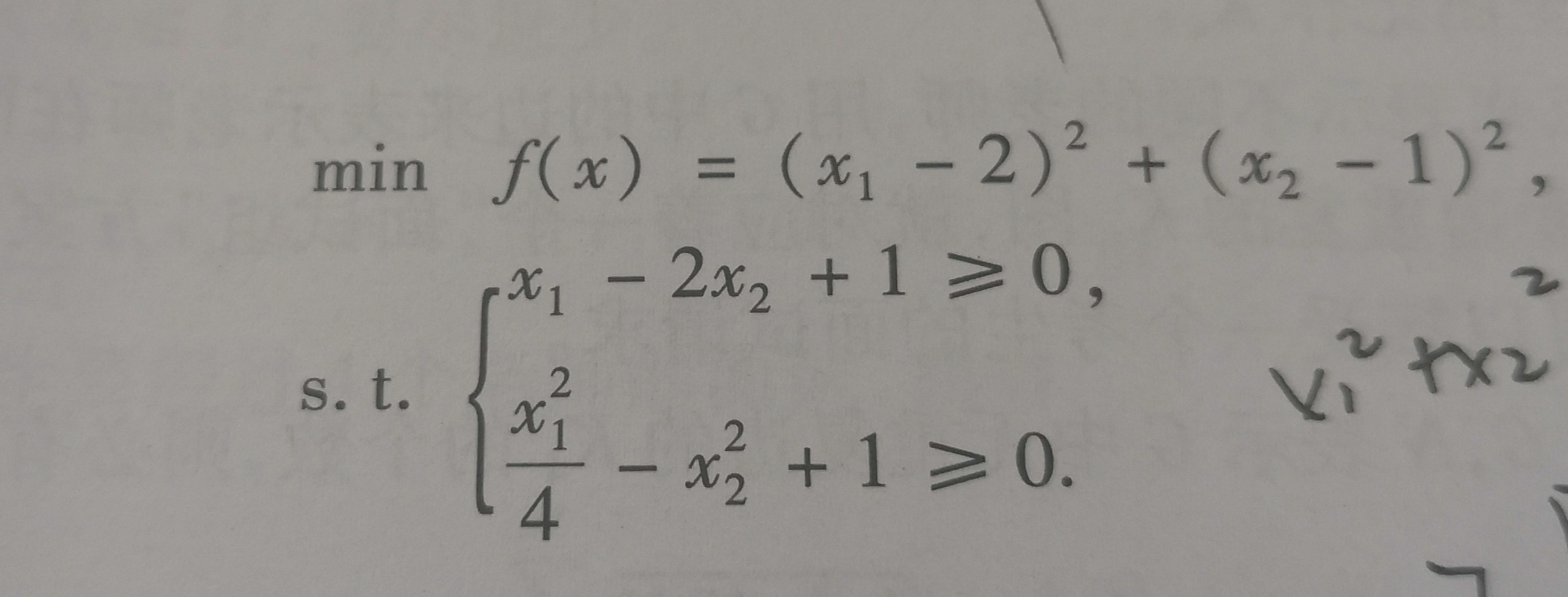
解法一:
ycfun1:
function y =yfun1(x); %这里申明是x的变量函数,则x(1)、x(2)就可以直接用了
%适应度函数
c1=[-4 -2];
c2=[1 1];
y=c1*x'+c2*x'.^2+5; %x的转置
ycfun2:
%非线性约束
function [f,g]=yfun2(x);%x为行向量
f=[-x(1)^2/4+x(2)^2-1];
g=[];
main:
clc,clear;
a=[-1 2];%线性约束
b=[1];%线性约束
[x,y]=ga(@yfun1,2,a,b,[],[],[],[],@yfun2);
x,y %输出x,y
结果集中在:
x =
2.0000 1.0000
y =
-8.8818e-16
解法二:
function ti12_1
fun1=@(x)(x(1)-2)^2+(x(2)-1)^2;
a=[-1,2];b=1;
[x,val]=ga(fun1,2,a,b,[],[],[],[],@fun2)
function [c,ceq]=fun2(x);
c=-x(1)^2/4+x(2)^2-1;
ceq=[];
以上两种解法不过是解法二将函数集中在一起写了而已。虽然解法二结果浮动较大,但是明显解法二的结果最优,其多次求解的值集中在e-21数量级。但是同样调用的是ga函数,为什么解法一的结果就始终集中在 -8.8818e-16?这个问题有待思考。