Lucas&ExLucas

---

Lucas：

公式：

C(n,m)%mod=C(n%mod,m%mod)*C(n/mod,m/mod)

需要保证mod为质数
证明省..

解决：
前面部分可以根据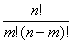

直接求出 

后面部分就继续递归

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
long long n,m,mod,fac[N];
void init()
{
    int i;
    fac[0] =1;
    for(i =1; i <= mod; i++)
        fac[i] = fac[i-1]*i % mod;
}
long long q_pow(long long a, long long b)
{
    long long  ans =1;
    while(b)
    {
        if(b &1)  ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;   
    }
    return  ans;
}
long long C(long long n, long long m)
{
    if(m > n)  return 0;
    return  fac[n]*q_pow(fac[m]*fac[n-m],mod-2) % mod;
}

long long Lucas(long long n, long long m )
{
    if(m==0)  return 1;
    return(C(n%mod,m%mod)*Lucas(n/mod m/mod))%mod;
}
int main()
{
    freopen("a.in","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%lld%lld", &n, &m, &mod);
        init();
        printf("%lld
",Lucas(n, m));
    }
    return 0;
}

---

 EX Lucas

解决mod不为质数的情况
我们先要求C(n,m)%mod
看到这个形式 我们可以考虑用中国剩余定理来求解
但是CRT也需要mod两两互质
怎么办？
我们把mod拆开modi=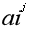ai为质数，表示多个幂相乘

这样modi的两两互质 可以用CRT了
现在就可以 求出C(n,m)%modi 然后CRT合并
但是现在modi 虽然ai是质数 但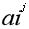却不是质数 

依然不能用Lucas求解(Lucas需要保证mod质数）

现在考虑C(n,m)%modi(modi不为质数) 怎么求？
我们把C(n,m)变成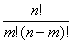如果我们能求出a=n!%modi,b=m!%modi,c=(n-m)%modi

那么最后答案就是a*inv(b)*inv(c)%modi

举个例子:

n=19,a=3,i=2
我们求n!%modi
(1*2*3*4*5*6*7*8*9*10*11*12*13*14*15*16*17*18*19)%modi
我们把它分成三部分
1. (1*2*4*5*7*8)*(10*11*13*14*16*17)
2. (3*6*9*12*15*18)=(3^6)*(1*2*3*4*5*6)
3. 19

我们可以发现一些规律
1 是一个以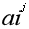为周期的循环节 在%modi后的值是相同的

解决方法：找出循环值和次数(n/3^6） 快速幂求解
2 可以把(3^6)拿出来 可以代入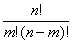上下抵消 剩下的部分是(n/a)! 变成同样的问题 可以继续递归解决

3 这是没有完成的一周期 我们暴力求得即可

#include<bits/stdc++.h>
using namespace std;

long long read()
{
    long long x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
long long mod,n,m,w;

long long qpow(long long a,long long b,long long p)
{
    long long ans=1LL;
    while(a>0)
    {
        if(a&1) ans=(ans*b)%p;
        b=(b*b)%p;
        a>>=1;
    }
    return ans;
}

void exgcd(long long a,long long b,long long &x,long long &y)
{
    if(b==0) {x=1;y=0;return ;}
    exgcd(b,a%b,x,y);
    long long temp=x;
    x=y;
    y=temp-a/b*y;
}

long long inv(long long a,long long p)
{
    long long x,y;
    exgcd(a,p,x,y);
    x=(x%p+p)%p;
    if(!x) x=p;
    return x;    
}

long long Mul(long long n,long long pi,long long pk)
{
    if(!n) return 1LL;
    long long ans=1LL;
    if(n/pk) 
    {
        for(long long i=2;i<=pk;i++) if(i%pi) ans=(ans*i)%pk;
        ans=qpow(n/pk,ans,pk);
    }
    for(long long i=2;i<=n%pk;i++) if(i%pi) ans=(ans*i)%pk;
    return (ans*Mul(n/pi,pi,pk))%pk;
    
}

long long C(long long n,long long m,long long pi,long long pk)
{
    if(n<m) return 0;
    long long a=Mul(n,pi,pk),b=Mul(m,pi,pk),c=Mul(n-m,pi,pk);
    long long k=0;
    for(long long i=n;i;i/=pi) k+=i/pi;
    for(long long i=m;i;i/=pi) k-=i/pi;
    for(long long i=n-m;i;i/=pi) k-=i/pi;
    long long ans=((a*inv(b,pk)%pk*inv(c,pk)%pk)%pk*qpow(k,pi,pk))%pk;
    return ans*(mod/pk)%mod*inv(mod/pk,pk)%mod;//mod/pk对pk的逆元
    
}

long long Lucas(long long n,long long m)
{
    long long ans=0;
    long long x=mod;
    for(long long i=2;i<=x;i++)
    {
        long long pk=1;
        if(x%i==0) 
        {
            while(x%i==0) pk*=i,x/=i;
            ans=(ans+C(n,m,i,pk))%mod;
        }
    }
    return ans;
}

int main()
{
    freopen("a.in","r",stdin);
    
    mod=read();n=read();m=read();
    long long ans=1;
    for(int i=1;i<=m;i++) 
    {
        w=read();
        if(n<w) {printf("Impossible
");return 0;}
        ans=(ans*Lucas(n,w))%mod;
        n-=w;
        printf("%lld %lld
",n,ans);
    }
    printf("%lld
",ans);    
    return 0;
}

---