从文本聚类到淘宝中“宝贝印象”服务的实现

“宝贝印象”是从用户评论中解析出关键词来，并根据这些关键词对于文档本身进行聚类以提供给用户更加直观评论信息。 淘宝系统当中有庞大的词库支持，如用户描述“好闻”“很香”等会被自动判断为“气味”，当该属性的提及次数在所有的属性词当中排在前K个，即会被展现，用户点击“气味”时，也会自动反向匹配相关评论的原文。

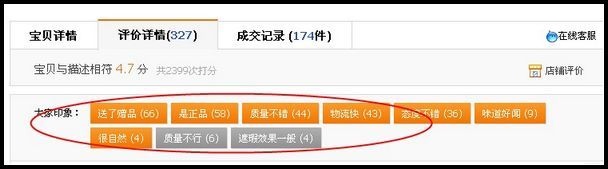
要实现这样的效果，首先需要对于关键词进行聚类。假设有一个documents－terms所组成的矩阵

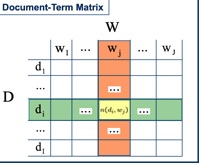
每一行代表一个文档，行当中的每个元素代表某个单词出现的次数，这样把字典中的所有单词全部平铺开来，就会形成一个很大而且稀疏的矩阵。假设该矩阵为A， 如果对这个矩阵进行SVD分解，则会得到如下的形式化表达：

其中U为AAT 的特征矩阵，而V为ATA的特征矩阵 由于特征矩阵表示了矩阵在现行空间内进行线性变换的本质（既沿着特征向量的方向拉伸或收缩特征值的倍数），所以U表示了现行空间内文档与文档之间的相似度关系，V表示了线性空间内单词与单词的相似度关系。（这里的所谓相似度，就是当两个词在同一个文档中同时出现的越频繁，就认为这两个词的相似度越大） 然而，对于A矩阵来讲，在现实的训练中可能会存在一些问题。首先，A矩阵会非常的大，且不论存储一个如此巨大的矩阵是否现实，单在计算矩阵的特征值以及特征向量时就是非常耗时的，并且无法进行并行化计算。其次，A矩阵包含了大量的噪声数据，这样得到的SVD分解结果可能并不能真正的对现实世界建模。第三，受限于训练数据的规模，该矩阵可能无法包含所有语言中的情况，这样在处理新的文档时，可能会存在一些无法处理的情况。第四，正如前面所说，该矩阵非常的稀疏。 基于以上的一些原因，在现实中应用SVD分解来得到文档或单词的聚类结果并不是一种非常可行的选择。Hofmann在SIGIR’99上提出了基于概率模型的PLSA模型，通过EM算法对该模型进行求解。 对于聚类的词汇来说，每一类可以认为是一个topic，它们描述了一个共同的概念。 PLSA是将文档，topic以及单词描述成为一个概率生成模型。假设D代表文档，Z代表Topic，W代表单词，那么，他们之间的概率生成关系可以用下图表示：

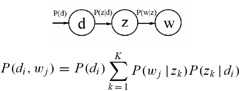
P(d)表示文档的先验概率，P(Z|D)表示文档中出现topic Z的概率，而P(W|Z)表示给定主题Z出现单词W的概率。通过这个概率图，引入了一个隐藏层Z，其关系如下图所示：

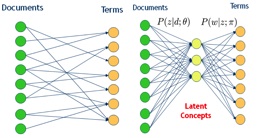
我们需要得知P(Z|D)以及P(W|Z)两组概率分布，而计算这两组分布可以通过EM算法进行求解。通过最大似然方法对于这个问题进行求解，可以得到如下的似然函数：

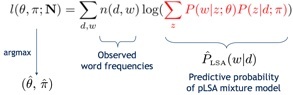
EM算法的基本步骤是：

1. 初始化对于训练样本概率模型的估计参数。
2. E：求隐含变量在当前估计参数条件下的后验概率。

                

　　3. M：最大化全部变量在当前数据下的期望。

　　　　　　

并行化的EM算法：

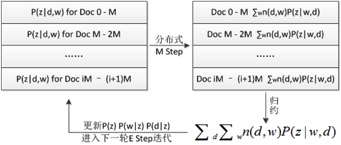
1. 初始化P(w|z) , P(z|d) 矩阵，将机器本地的相关矩阵归一化
2. 对本地文档执行E步骤
3. 仅对本地计算好的P(z|d,w) 执行M步骤
4. 同步所有的机器，汇总全部的P(z|d,w)值
5. 继续执行第二步

回到前面说的“宝贝印象”的实现上。对于某一个商品中的所有评论，首先做切词处理。然后，按照字典可以计算每个topic在评论中被提及了多少次以及每个文档涉及到哪些topic。之后，将被提及频率最高的K个topic提取出来做为展示结果。对于每个文档来说，可以简单的根据其包含的topic数量与频率来判断其属于哪个topic。这样就可以得到这种评价聚类的展示效果。所展示的词，是topic的代表词，可以通过人工标签的方式进行指定。

在进行PLSA训练的过程中，一个最大的问题是如何确定所训练出来的模型的好坏。一般的，可以通过计算PMI－SCORE来进行评测。 PMI-SCORE的原理很简单。一般来说，人工评判一个聚类模型的效果是否明显采用对一个topic中概率最大的10个词是否相关。对于计算机来说可以通过对一个topic中所有的词做相关性的统计来实现。评估所采用的数据是来自训练文本之外的文本，这样可以很好的规避训练数据中的噪音。采用一定大小的滑动窗口就可以对两个单词的“同现”概率进行统计。选取同一个topic中所有共现词共现概率的中位数作为该topic的PMI－SCORE。 PMI-Score(w) = median{PMI(wi,wj), ij 2 1 . . . 10},

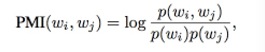
如图所示，假设该图描述的是五个单词“music band rock dance opera”组成的topic，其共现概率为边的权值。则该topic的PMI-SCORE为3.1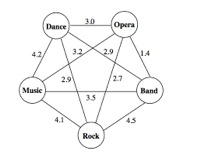

对训练好的模型求PMI-SCORE，选取值大的那一种做为最终的训练结果。

相关文章：

http://www.ics.uci.edu/~newman/pubs/Newman-ADCS-2009.pdf 关于PMI-SCORE的评判

Hofmann, Probabilistic Latent Semantic Indexing, ACM SIGIR, 1999. 提出PLSA的论文

T. Hofmann, Probabilistic Latent Semantic Analysis, Uncertainty in AI, 1999 T.

Hofmann, Unsupervised Learning by Probabilistic Latent Semantic Analysis, Machine Learning Journal, 2000.

T. Hofmann, J. Puzicha, P. Tufts, Finding Information: Intelligent Retrieval & Categorization, Whitepaper, Recommind, December 2002

LDA（另一种Topic Model）相关的文章

T. Minka and J. Lafferty, Expectation-propagation for the generative aspect model, UAI 2002.

D. M. Blei and A. Y. Ng and M. I. Jordan, Latent Dirichlet allocation, J. Mach. Learn. Res., vol 3, 993—1022, 2003.

W. Buntine, Variational Extensions to EM and Multinomial PCA, ECML, 2003.