前置芝士
了解堆。
引言
如果要求你合并两个优先队列,并且合并后的结果仍然符合优先队列的性质,此时怎么做?
显然,此处不能使用普通的堆。那如何完成操作呢?这时候就需要使用一种特殊的堆了:左偏树。
正文
左偏树的名,乍一听,像是棵向左偏的树。实际上它的确是一棵向左偏的树(雾),但是向左偏的并不是节点。具体是什么“左偏”会在下文中讲解。
概念定义
外节点
当且仅当此节点的左子节点和右子节点中的一个是空节点,或者左子节点和右子节点都是空节点,该节点才能被称作外节点。
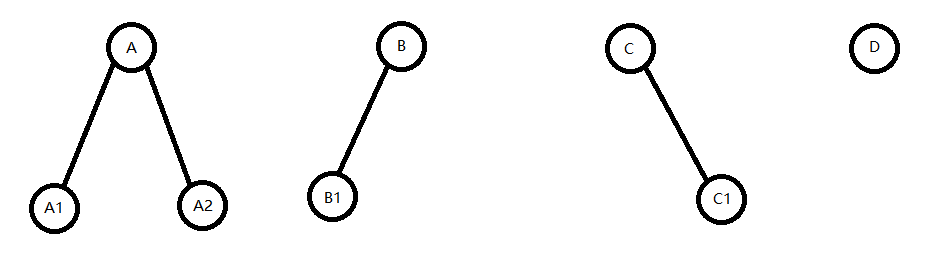
如图:A节点不属于外节点,因为它有左右子节点;B、C节点属于外节点,因为B节点没有右子节点,C节点没有左子节点;D节点也属于外节点,因为它没有左右子节点。
距离
左偏树中,点的距离为该点到它的子树中,离它最近的外节点的距离。
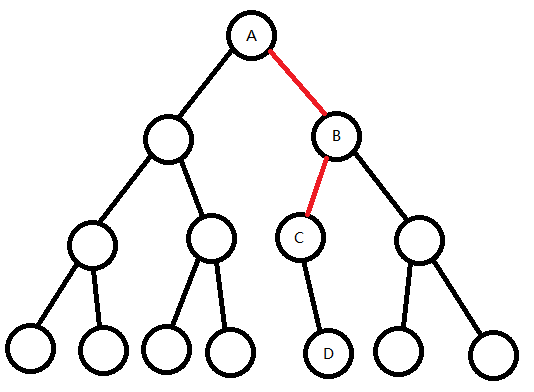
该图中,离根节点最近的外节点为 (C) 。(A → B → C) 需经过两个节点,所以根节点 (A) 的距离为2。
性质与推论
一颗左偏树,必须有如下两个性质:
· 性质一. 任意节点的权值都要小于其父节点(如果有的话)的权值;
· 性质二. 任意节点的左子节点的距离一定大于右子节点的距离;
根据性质,可以得到如下推论:
· 推论一. 任意一个非外节点的距离为其右子节点的距离 + 1;
· 推论二. (n) 个点的左偏树的最大距离为 (log(n + 1) - 1。)
推论一给出了更新节点距离的方法,而推论二保证了左偏树的时间复杂度。
操作
合并(merge)
快速合并两个普通堆基本是天方夜谭,但合并操作在左偏树中的重要性不亚于splay操作在Splay中的重要性,所以请读者务必理解这一模块。
假设现在给定两棵左偏树,(a, b) 是它们的根节点,现在要将 (b) 合并到 (a) 上。
根据堆最基础的性质(根节点的权值应小于子节点的权值),(b) 的权值应小于当前遍历到的点(以下称其为 (x) )。故如果遇到 (val_x < val_b) 的情况,则要将 (x) 与 (b) 调换。
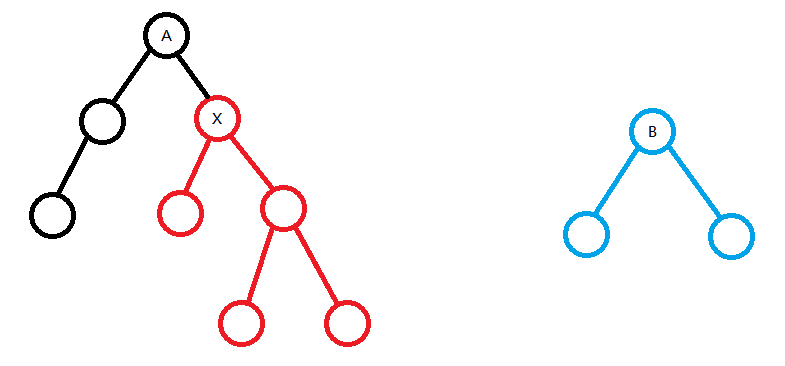
假设 (val_x > val_b) ,则此时应将 (x) 与 (b) 调换。
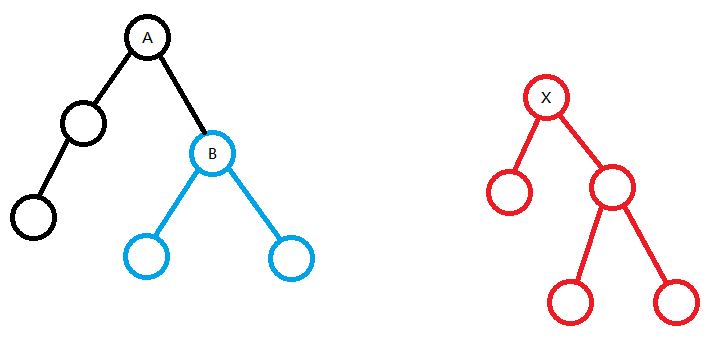
调换完成后,继续向右子节点递归,直到当前节点没有右子节点、或者 (b) 被清空。回溯的过程中,更新左右子节点的距离并判断是否满足性质二,若不满足则需调换左右子节点,直到回溯到根节点。
inline int merge (int x, int y) { //合并两棵树
if (!x) //若该节点无左儿子,则返回右子树;下同
return y;
if (!y)
return x;
if (val[x] > val[y] || (val[x] == val[y] && x > y)) //若左右节点的val值出现矛盾,则进行置换操作
swap (x, y);
sons[x][1] = merge (sons[x][1], y); //从右子节点开始进一步进行合并操作
if (dis[sons[x][1]] > dis[sons[x][0]]) //若x,y节点的距离值矛盾,则置换
swap (sons[x][0], sons[x][1]);
fa[sons[x][0]] = fa[sons[x][1]] = fa[x] = x; //路径压缩
dis[x] = dis[sons[x][1]] + 1; //更新距离值
return x;
}
加入单个节点(push/add)
将单个节点当成只有一个节点的左偏树进行合并。
inline int add (int value, int x) { //增加一个节点,以子树形式加入
cnt ++;
sons[cnt][0] = sons[cnt][1] = dis[cnt] = 0;
val[cnt] = value;
return merge (cnt, x); //将单独的节点以子树形式合并入整棵树
}
弹出根节点(pop/del)
清空根的信息,将根的左右子节点的父亲值改为自身,再进行合并。
inline void del (int x) { //删除根节点
int l = sons[x][0], r = sons[x][1];
val[x] = -1;
fa[l] = l;
fa[r] = r;
fa[x] = merge (l, r); //合并左右子节点
return ;
}
建立左偏树(build)
将所有节点压入一个队列,每次取出队列头的两个节点,进行合并后,将新根节点压入队列最末端,直到队列只剩一个元素(总根)。
inline int build () { //建造左偏树
queue <int> q;
for (int i = 1; i <= n; i ++) //将节点压入序列中
q.push (i);
while (!q.empty ())
if (q.size () == 1)
break ;
else { //每次将队首的两个节点当作两颗子树进行合并,将得到的新子树再压入队列
int x = q.front (); q.pop ();
int y = q.front (); q.pop ();
q.push (merge (x, y));
}
int rt = q.front (); q.pop (); //更新根节点
return rt;
}
总代码
可以在 Luogu3377 上提交。
//例题并没有用到所有的函数,建议读者打完板子后,自行测试所有函数的正确性。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5, INF = INT_MAX;
int n, m, cnt, a[N], fa[N], dis[N], val[N], sons[N][2];
//cnt:当前节点数; fa[x]:x的父节点; dis[x]:x的距离; val[x]:x节点的值; sons[x][y]:x节点的y儿子
inline int find (int x) { //寻找祖父节点
if (fa[x] != x)
return fa[x] = find (fa[x]); //注意此处要路径压缩,否则会在最后一个点超时
return x;
}
inline int merge (int x, int y) { //合并两棵树
if (!x) //若该节点无左儿子,则返回右子树;下同
return y;
if (!y)
return x;
if (val[x] > val[y] || (val[x] == val[y] && x > y)) //若左右节点的val值出现矛盾,则进行置换操作
swap (x, y);
sons[x][1] = merge (sons[x][1], y); //从右子节点开始进一步进行合并操作
if (dis[sons[x][1]] > dis[sons[x][0]]) //若x,y节点的距离值矛盾,则置换
swap (sons[x][0], sons[x][1]);
fa[sons[x][0]] = fa[sons[x][1]] = fa[x] = x; //路径压缩
dis[x] = dis[sons[x][1]] + 1; //更新距离值
return x;
}
inline int add (int value, int x) { //增加一个节点,以子树形式加入
cnt ++;
sons[cnt][0] = sons[cnt][1] = dis[cnt] = 0;
val[cnt] = value;
return merge (cnt, x); //将单独的节点以子树形式合并入整棵树
}
inline void del (int x) { //删除根节点
int l = sons[x][0], r = sons[x][1];
val[x] = -1;
fa[l] = l;
fa[r] = r;
fa[x] = merge (l, r); //合并左右子节点
return ;
}
inline int build () { //建造左偏树
queue <int> q;
for (int i = 1; i <= n; i ++) //将节点压入序列中
q.push (i);
while (!q.empty ())
if (q.size () == 1)
break ;
else { //每次将队首的两个节点当作两颗子树进行合并,将得到的新子树再压入队列
int x = q.front (); q.pop ();
int y = q.front (); q.pop ();
q.push (merge (x, y));
}
int rt = q.front (); q.pop (); //更新根节点
return rt;
}
int opt, firs, seco;
int main () {
scanf ("%d%d", &n, &m);
dis[0] = -1;
for (int i = 1; i <= n; i ++) {
scanf ("%d", &val[i]);
fa[i] = i;
}
for (int i = 1; i <= m; i ++) {
scanf ("%d", &opt);
if (opt == 1) {
scanf ("%d%d", &firs, &seco);
int xx = find (firs), yy = find (seco);
if (val[firs] == -1 || val[seco] == -1 || xx == yy)
continue ;
else
fa[xx] = fa[yy] = merge (xx, yy);
} else {
scanf ("%d", &firs);
if (val[firs] == -1)
puts ("-1");
else {
int rt = find (firs);
printf ("%d
", val[rt]);
del (rt);
}
}
}
return 0;
}