问题描述:给出一个非负整数num,对[0, num]范围内每个数都计算它的二进制表示中1的个数
Example:
For num = 5 you should return [0,1,1,2,1,2]
思路:该题属于找规律题,令i从0开始,设f(i)为i对应二进制表示中1的个数,写几对对应值就出来了。
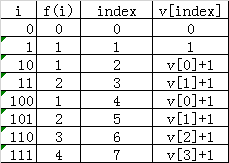
很明显,规律就是[0, 1)部分各个值加1就构成了[1, 2)部分,[0, 2)部分各个值加1就构成了[2, 4)部分,[0, 4)部分各个值加1就构成了[4, 8)部分。
以此类推。
原因也很显然,是最高位的1,使二进制中1的个数多了1。
也就是从初始状态res = {0}, n = 1开始:
每次新增长度与res相等的序列newSeq,满足newSeq[i] = res[i] + 1,i = 0, 1, 2, …… , 2^(n-1)-1
然后把newSeq添加到res末尾。依次循环直到长度大于num+1。
其中res长度的增长过程是1——2——4——8——……——log2(num+1)——num。除了最后一步都是加倍增长。
解法:
刚开始试着用链表list来动态增加(splice),把原来的list(l0)每个值都加1后构成新的list(l1),然后把l1插入到l0末尾。
这样l0大小从1到2到4到8……一直到log2(len),再把剩下的len - log2(len)个元素构成新的list(l1)插入到末尾。
class Solution {
public:
vector<int> countBits(int num) {
int len = num + 1;
list<int> l0 = { 0 };
int n = 1;
bool b = true;
while (n < len) {
if (len - n < n) {
int newCnts = len - n;
auto it = l0.cbegin();
for (int i = 0; i < newCnts; ++i) {
l0.push_back(1 + *it++);
}
break;
} else {
list<int> l1;
auto it = l0.cbegin();
while (it != l0.cend())
l1.push_back(1 + *it++);
l0.splice(l0.end(), l1);
n *= 2;
}
}
vector<int> res(len);
auto it1 = l0.cbegin();
auto it2 = res.begin();
while (it2 != res.end())
*it2++ = *it1++;
return res;
}
}; // 15/15 96ms 20.09%
然后发现代码又长,效率不怎样,这里splice比起在vector中计算元素的位置没有什么优势,问题在于每次push_back都要新申请一个元素的空间,最后还要重新转换成vector(PS:leetcode给出的C++函数签名的返回值是vector),这种靠链接list的小伎俩还不如老老实实用vector。(好吧我承认是被STL的list排序算法影响到了……)
于是用vector写了下,代码变短了而且效率还可以(目测可以精简下代码)
class Solution {
public:
vector<int> countBits(int num) {
const int len = num + 1;
vector<int> res(len);
int nb = 1;
int ne = nb << 1;
res[0] = 0;
while (ne < len) {
for (int i = nb; i < ne; ++i)
res[i] = res[i - nb] + 1;
nb = nb << 1;
ne = nb << 1;
}
for (int i = nb; i < len; ++i)
res[i] = res[i - nb] + 1;
return res;
}
}; // 15/15 88ms 53.16%
试着改进了下,就是对于每个新的序列,比如[4, 8)对应{1, 2, 2, 3},[1, 4)对应{0, 1, 1, 2}
[4, 6)区域和[2, 4)区域的值是一样的,而[6, 8)区域的值是[2, 4)区域对应值加1。这样每次遍历[nb + (ne-nb)/2, ne)再运算两次即可,用temp保留遍历的值,temp和temp+1赋给新的位置。这样省去了一次+1操作。
但是问题是这样增加了一次赋值操作,测试运行时间是一样的,暂时就此打住吧,有空再看看优秀解法。