a. 一元高斯分布
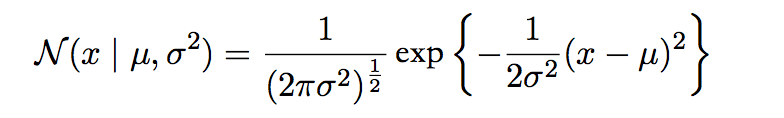
b. 多元高斯分布
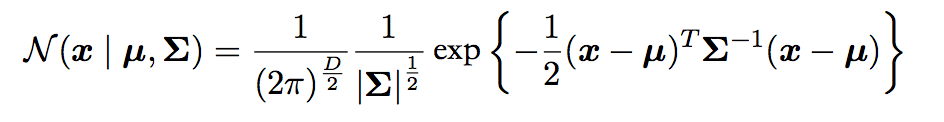
c. 似然函数
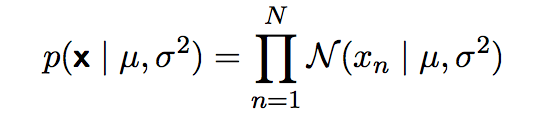
d. 独立同分布(i.i.d —> independent and identically distributed)
给定一个样本集合,其中样本都取自于同一个分布,且彼此之间相互独立,称之为独立同分布;其特性就是这些样本的联合概率,为它们各自的边缘分布的乘积;
e. 最大似然估计的局限性
基于给定样本集合来估计分布(求解分布参数),常用的方法是最大似然估计法,即选择这样的分布参数,它能使得样本的联合概率最大。(疑惑:不是应该基于给定的样本数据,选择概率最大的分布参数么,两者有什么区别呢?)
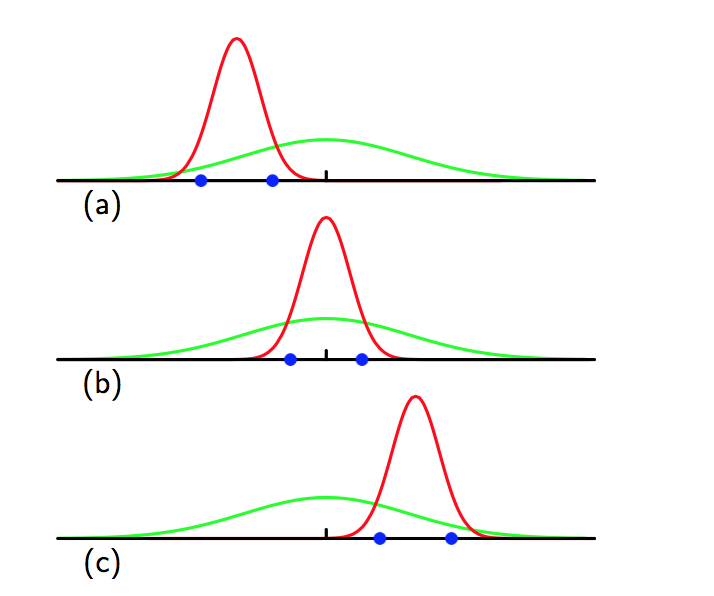
三个样本集合取自同一个高斯分布,分别对应上图中的(a)(b)(c),可以看出:
(1)多次抽样产出,样本均值的期望等于真实分布的均值;
(2)由于样本方差是由当前样本均值得到,故即便多次抽样,样本方差的期望较真实分布的方差偏小;
上述情况就是所谓的偏置现象,这也是过拟合的本质原因。