0. 写在最前面
很久之前学的,找了网上都是一些“温度计”的例子,看到都快吐了。找了很久,看到一些讲解,尤其英文的 讲解,非常有用。当时总结了一些,最近复习看了《Probabilistic Robotics》觉得又加深了一点认识,在这里总结一下~~~要求大家懂一点现代控制理论的知识,或者基本的矩阵运算知识。
1. 卡尔曼滤波的三个假设
- 服从高斯分布(测量噪声、系统噪声以及初始值都要求是,且互不相关)
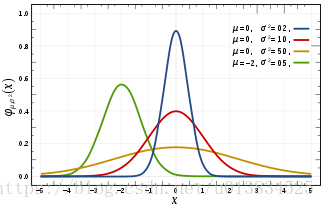
高斯分布又叫正态分布,其概率密度函数服从,其中μ是均值,σ2是方差。不同参数得到的函数如下,方差描述了该分布的集中程度,方差越大,函数越矮胖。如果是测量噪声用高斯分布描述的话,方差越大,表明传感器越不精准。
- 系统是线性的(状态变化和测量都要求是)
要求满足如下方程,其中是状态向量,F是状态转移矩阵,B是控制输入矩阵,w是过程噪声向量;z是测量向量,H是测量矩阵,v是测量噪声向量。
- 贝叶斯滤波的马尔可夫假设
又叫完整状态假设,假设过去以及未来的数据都是独立的。也就是t时刻的状态可以只由t-1时刻的状态推出,与0-(t-2)时刻的状态无关。这个其实在上面的线性公式中已经体现出来了。
2. 直观解释与应用例子
给出了一些链接或者论文题目,建议看完后面的公式以及推导等再回来详细看,现在有个印象即可。
2.1 两个噪声呈高斯分布的测量互补融合成一个相对准确的高斯分布
- 比如平衡车中,使用陀螺仪积分可以得到倾角,使用加速度计也可以计算得到倾角,两个的精度都不高,比较难满足要求。所有可以假设两者的噪声都满足高斯分布的假设,然后用卡尔曼互补滤波来生成一个更加精确的倾角数据。(如郑慧伟等人的《卡尔曼滤波在二轮自平衡车直立控制中的应用 》)
- 再比如飞行器上,我们可以利用GPS进行定位,也可以利用惯性测量组合(MIMU)来进行定位。最后假设 两者的噪声都满足高斯分布的假设,再利用卡尔曼互补滤波来得到相对更精确的定位。(如徐华中等人的《卡尔曼滤波在四轴飞行器导航中的应用 》)
2.2 卡尔曼滤波本质上是贝叶斯滤波的一种矩参数实现
有兴趣可以看看《Probabilistic Robotics》中的详细说明,没兴趣了解的只需要记着就好。其实下面说的也是两个高斯分布的融合,只不过看待问题的角度不一样罢了。

- 比如一辆直线行走的小车,我们可以通过编码器或者加速度计甚至可以根据上一时刻的位置速度估计出当前时刻的位置。但是轮子会打滑,编码器的测量等也可能很不准,只能得到小车的先验估计位置。这时候有一个激光测距可以测得到小车的距离,但是有噪声。就可以通过卡尔曼滤波来得到相对准确的后验位置。(如《Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation 》这篇文章)
- 再比如经典的温度的例子,知道上一时刻的温度,可以根据温度的变化趋势预估当前时刻的温度,但这很不准确,只是先验。然后我们用一个温度计测量得到当前的温度,通过卡尔曼滤波可以得到温度的后验估计。
- 再比如图像处理中,用卡尔曼进行目标跟踪。已知上一时刻的位置,我们可以认为目标的位置没有变动,或者之前的速度方向变动了一点点,得到先验估计。然后我们运行目标检测程序,得到该目标在图象上的位置。( 如史国荣等人的《基于卡尔曼预测和滤波的视频目标跟踪 》、曲云腾 等人的《基于 Kalman 预测的人体运动目标跟踪 》)
贝叶斯滤波的先计算得到先验概率,然后计算后验概率,跟卡尔曼的先通过状态转移与运动方程估计先验状态,再根据观测方程得到后验状态,简直一毛一样。
2.3 为什么不直接用观测结果
到了这里,肯定很多人会有疑问,为什么我不直接用测量的结果?加速度计或者陀螺仪,我哪个准确用哪个呗;GPS和MIMU哪个准确用哪个呗;小车那个直接用激光测距的值不就行了了;温度直接用温度计的不是更好吗;图像检测到的位置就是准确位置啊,预测什么预测。
但大家忽略了一点,任何传感器都是有噪声的、任何的目标检测算法都是有误差的。而上面说过,两个高斯分布的乘积,其不准确性是比这两个高斯分布都要低的。也就是,卡尔曼滤波的结果会比两个测量的都要好!!!这才是最关键的。而且其协方差是动态的,如果有一个测量100%准确,而另一个测量不是很准确,那最终卡尔曼也会收敛到这个100%准确的传感器的值。
3. 公式与推导
其中
X:状态向量 F:状态转移矩阵
B:控制输入矩阵 u:控制向量
P:总协方差矩阵 Q:过程噪声协方差矩阵
R:测量噪声协方差矩阵 H:转移矩阵(将测量值转换成状态)
K:卡尔曼增益 z:测量值
最近比较忙,等有时间会将数学推导及示例代码整理出来,稍等!