1038. 把二叉搜索树转换为累加树
题目链接
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目描述
给定一个二叉搜索树,请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意:该题目与 538: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ 相同
示例 1:
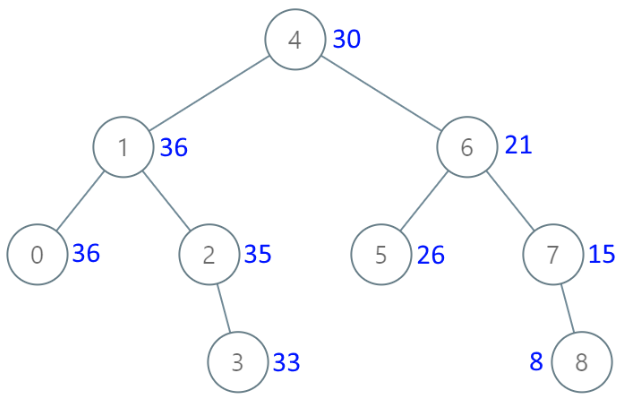
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于 1 和 100 之间。
- 每个节点的值介于 0 和 100 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
题目分析
- 根据题目描述,将二叉搜索树转换为累加树,
- 累加树是将二叉搜索树按照中序排列,如示例1中的二叉搜索树按照中序展开为[0, 1, 2, 3, 4, 5, 6, 7, 8],从后向前一次累加,即累加树的中序展开为[36, 36, 35, 33, 30, 26, 21, 15, 8]
- 使用深度优先搜索按照先右子树、再根节点、后左子树的顺序遍历二叉搜索树,依次记录累加的和,改变节点的值
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* bstToGst(TreeNode* root) {
dfs(root, 0);
return root;
}
private:
int dfs(TreeNode* root, int val) {
if (!root) return val;
int right = dfs(root->right, val);
root->val += right;
int left = dfs(root->left, root->val);
return left;
}
};