99. 恢复二叉搜索树
题目链接
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/recover-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目描述
给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗?
示例 1:
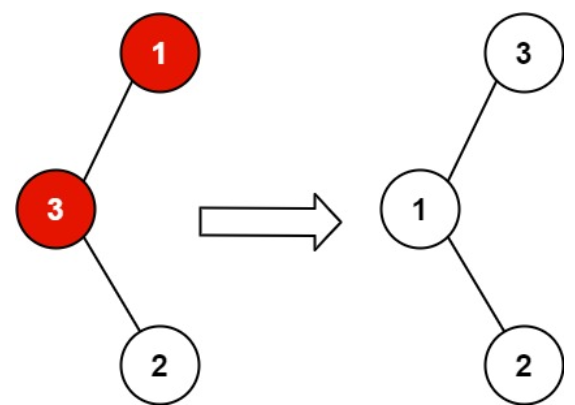
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
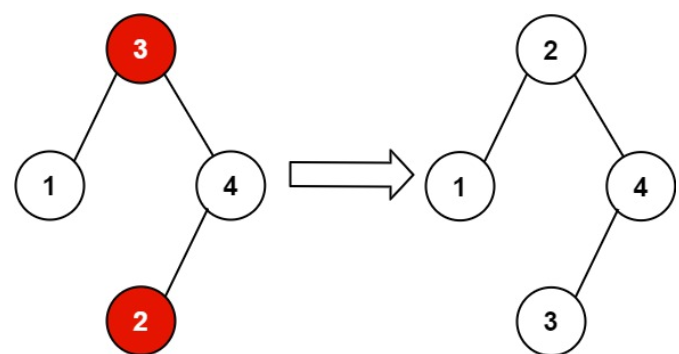
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
- 树上节点的数目在范围 [2, 1000] 内
- -231 <= Node.val <= 231 - 1
题目分析
- 根据题目描述将二叉树恢复为二叉搜索树
- 中序遍历二叉树,获取二叉树的无序序列
- 再将无序序列排序为有序序列,再次中序遍历二叉树修改每个节点的值
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void recoverTree(TreeNode* root) {
vector<int> nums;
getVal(nums, root);
sort(nums.begin(), nums.end());
int index = 0;
setVal(root, nums, index);
return;
}
private:
void getVal(vector<int>& nums, TreeNode* root) {
if (root == nullptr) return;
getVal(nums, root->left);
nums.push_back(root->val);
getVal(nums, root->right);
return;
}
void setVal(TreeNode* root, vector<int>& nums, int& index) {
if (root == nullptr) return;
setVal(root->left, nums, index);
root->val = nums[index++];
setVal(root->right, nums, index);
return;
}
};