Orthogonal table
概述
正交试验中使用的正交表的生成过程其实就是一个加法Abel群的生成过程。对于m水平表![]() 而言,为了方便起见我们对水平表的每个元素均做
而言,为了方便起见我们对水平表的每个元素均做![]() 的处理,任取其中的任意两列
的处理,任取其中的任意两列![]() 则一定具有完全对:
则一定具有完全对:
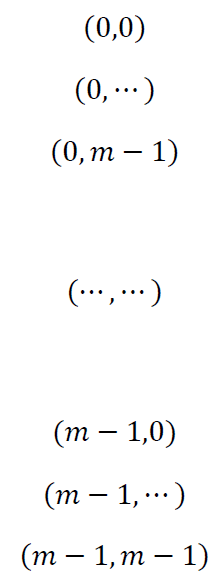
这说明a和b都是一个分量包含0~m-1的列向量,并且有:
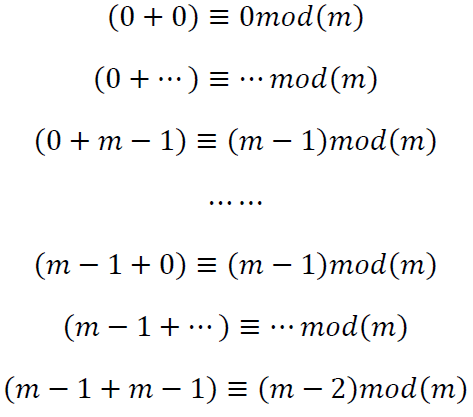
也就是说在 ![]() 上
上 ![]() 或者
或者 ![]() 也都具有完全对。
也都具有完全对。
至此我们可以定义加法:
![]()
对于标准表而言,若a和b是标准表![]() 的 2 个列,那么
的 2 个列,那么![]() 也一定是标准表
也一定是标准表![]() 的一个列。
的一个列。
有限Abel群的基底
考虑到标准表中任取 2 列的完全对出现的次数都是均等的 , 因此![]() 的列总是以
的列总是以
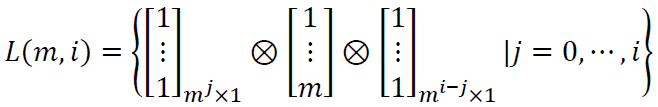
中的元素为基础关于![]() 运算生成的,其中
运算生成的,其中 ![]() 是矩阵的Kronecker乘积。
是矩阵的Kronecker乘积。
有限Abel群的子群
令G是以![]() 为基底,关于
为基底,关于![]() 运算生成的Abel群,则G明显是拥有众多Abel子群的,例如在确定G的基底是
运算生成的Abel群,则G明显是拥有众多Abel子群的,例如在确定G的基底是
![]()
的情况下,显然:
![]()
是G的子群。现在我们扩展一下这个系列。令:
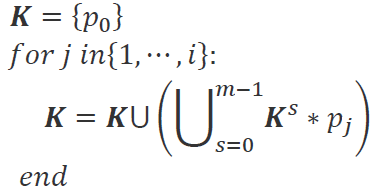
此时![]() 都是G的m阶循环子群。
都是G的m阶循环子群。
构造
Step1.K的全体元素就是正交表的所有列。正交试验标准表可按此法构造。
Step2.若有 ![]() ,则说明第i列和第j列对应放置交互作用的列应该是第
,则说明第i列和第j列对应放置交互作用的列应该是第![]() 列。正交试验表头可按照此法构造。
列。正交试验表头可按照此法构造。
后记
此法没有涉及任何的枚举过程,计算出的正交表和表头表的生成速度比正常枚举法要快非常多,正常的单线程运行此算法,一个行数和列数均在200以上的正交表只需要1秒不到就能算出。
值得注意的是Step2中所描述的正交表表头并非是一定能以此法完整的构造出的,因为Step2中的等号并非一定成立。为什么会出现这种情况呢,原因就是因为![]() 的构造方式并不能保证对于任意的i和j 都能找到
的构造方式并不能保证对于任意的i和j 都能找到![]() 使得Step2中等号都的成立。按照道理来说我们需要找一个只由
使得Step2中等号都的成立。按照道理来说我们需要找一个只由![]() 构造出的循环群
构造出的循环群![]() ,如果这样的
,如果这样的![]() 都能满足Step2中的等式,则正交表头可完整构造出来。
都能满足Step2中的等式,则正交表头可完整构造出来。
Python Code(import numpy)
1 class OrthogonalTableMap(): 2 3 def __init__(self, level, time): 4 self.m = level 5 self.time = time 6 n = self.m**(time + 1) 7 k = (n - 1)//(self.m - 1) 8 9 # 构造self.base,self.base的元素与加法群的基底一一对应 10 self.base = [numpy.zeros(n, numpy.int)] 11 for j in range(0, time + 1): 12 mat1 = numpy.ones(self.m**j, numpy.int) 13 mat2 = numpy.linspace(1, self.m, self.m, dtype = numpy.int) 14 mat3 = numpy.ones(self.m**(time - j), numpy.int) 15 self.base.append(numpy.kron(numpy.kron(mat1, mat2), mat3) - 1) 16 self.base = self.base[1:len(self.base)+1] 17 18 # 构造正交表self.table和记录每列群属性的self.dir 19 self.dir = [numpy.zeros((time + 1, self.m - 1), numpy.int)] 20 self.dir[0][0, 0] = 1 21 for j in range(1, self.m - 1): 22 self.dir[0][:, j] = (j + 1)*self.dir[0][:, 0]%self.m 23 24 self.table = [self.base[0]] 25 for j in range(1, time + 1): 26 self.table.append(self.base[j]) 27 28 self.dir.append(numpy.zeros((time + 1, self.m - 1), numpy.int)) 29 self.dir[-1][j, 0] = 1 30 for k in range(1, self.m - 1): 31 self.dir[-1][:, k] = (k + 1)*self.dir[-1][:, 0]%self.m 32 33 for k in range(0, len(self.table) - 1): 34 for s in range(1, self.m): 35 self.table.append((s*self.table[k] + self.base[j])%self.m) 36 37 self.dir.append(numpy.zeros((time + 1, self.m - 1), numpy.int)) 38 self.dir[-1][:, 0] = s*self.dir[k][:,0] 39 self.dir[-1][j, 0] += 1 40 self.dir[-1][:, 0] = self.dir[-1][:, 0]%self.m 41 for t in range(1, self.m - 1): 42 self.dir[-1][:, t] = (t + 1)*self.dir[-1][:, 0]%self.m 43 44 # 将self.base和self.table以矩阵形式表示,并且+1还原 45 temp = numpy.zeros((n, len(self.base)), numpy.int) 46 for j in range(0, len(self.base)): 47 temp[:, j] = self.base[j] 48 self.base = temp + 1 49 temp = numpy.zeros((n, len(self.table)), numpy.int) 50 for j in range(0, len(self.table)): 51 temp[:, j] = self.table[j] 52 self.table = temp + 1 53 54 # self.hash_dir的一个元素都是self.table的一个列对应的群成员的hash值集合 55 self.hash_dir = self.hash_function() 56 57 self.error = 0 58 59 def hash_function(self): 60 # 制作hash函数将self.dir所包含的信息处理成数据类型为numpy.int的基本元素的集合簇输出 61 mat = numpy.ones((1, self.time + 1), numpy.int) 62 for j in range(1, self.time + 1): 63 mat[0, j] *= self.m**j 64 hash_dir = self.dir.copy() 65 for j in range(0, len(self.dir)): 66 hash_dir[j] = set(numpy.dot(mat, self.dir[j]).reshape(self.m - 1)) 67 68 return hash_dir 69 70 def hash_add(self, var_set, format_check = True): 71 # 制作与向量加法对应在hash映射下的加法hash_add 72 if format_check: 73 if len(var_set)<2: 74 print("Error:var_set should at least has 2 elements.") 75 if max(var_set)>len(self.hash_dir) or min(var_set)<0: 76 print("Error:var_set's elements should between 0~len(hash_dir).") 77 arg_set = numpy.array(var_set) 78 79 var_out = 0 80 for j in range(0, self.time + 1): 81 temp = 0 82 for k in range(0, len(var_set)): 83 temp += arg_set[k]//self.m**(self.time - j) 84 var_out += (temp%self.m)*self.m**(self.time - j) 85 arg_set = arg_set%self.m**(self.time - j) 86 87 return var_out 88 89 def hash_set_add(self, sets_ind, end_set = None): 90 # 定义hash后的self.dir的集合对应在hash映射下的加法hash_set_add 91 if len(sets_ind)==0: 92 set_num = list() 93 for j in range(0, len(self.hash_dir)): 94 if len(self.hash_dir[j]&end_set)>0: 95 set_num.append(j) 96 return set_num 97 98 if end_set is None: 99 if len(sets_ind)<2: 100 print("Error:set_ind should at least has 2 elements.") 101 end_set = self.hash_dir[sets_ind[-1]] 102 sets_ind.pop() 103 104 temp_set = list() 105 for j in self.hash_dir[sets_ind[-1]]: 106 for k in end_set: 107 temp_set.append(self.hash_add([j, k], format_check = False)) 108 end_set = set(temp_set) 109 sets_ind.pop() 110 111 return self.hash_set_add(sets_ind, end_set) 112 113 def title(self): 114 # 使用矩阵title表示带有多因素交互作用的表头,若没有成功找到所有子群则修改self.error = 1 115 title = numpy.zeros((len(self.hash_dir)*(self.m - 1), 116 len(self.hash_dir)), numpy.int) 117 try: 118 for j in range(0, len(self.hash_dir)): 119 title[(self.m - 1)*j:(self.m - 1)*(j + 1), j] = j + 1 120 for k in range(j + 1, len(self.hash_dir)): 121 temp = numpy.array(self.hash_set_add([j, k])).reshape(self.m -1) 122 title[(self.m - 1)*j:(self.m - 1)*(j + 1), k] = temp +1 123 self.error = 0 124 except ValueError: 125 self.error = 1 126 return title
Demo
3水平13因素正交表(表头数据依赖于列排序,列排序不一定和文献资料一样,如需对照请自行重新排序对照)
ex = OrthogonalTableMap(3,2) print("table = ") print(ex.table) print("title = ") print(ex.title())
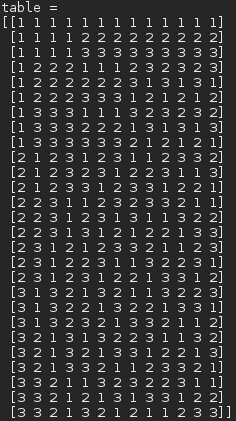
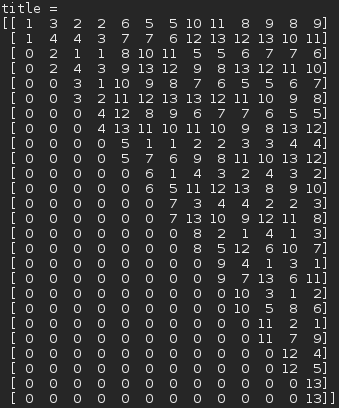
声明
本文由“Hamilton算符”原创,未经博主允许不得转载!