计算几何学习笔记（一）——Convex Hull

前言：

计算几何（cumputational Geometry）可以理解成在几何条件下进行的算法设计与分析，是计算机课程的基础课程，并且对于后续课程的学习有着重要的作用，例如图形学的学习，人工智能中的路径规划问题等等

凸包问题

1)问题导入

我们考虑这样的几个点：

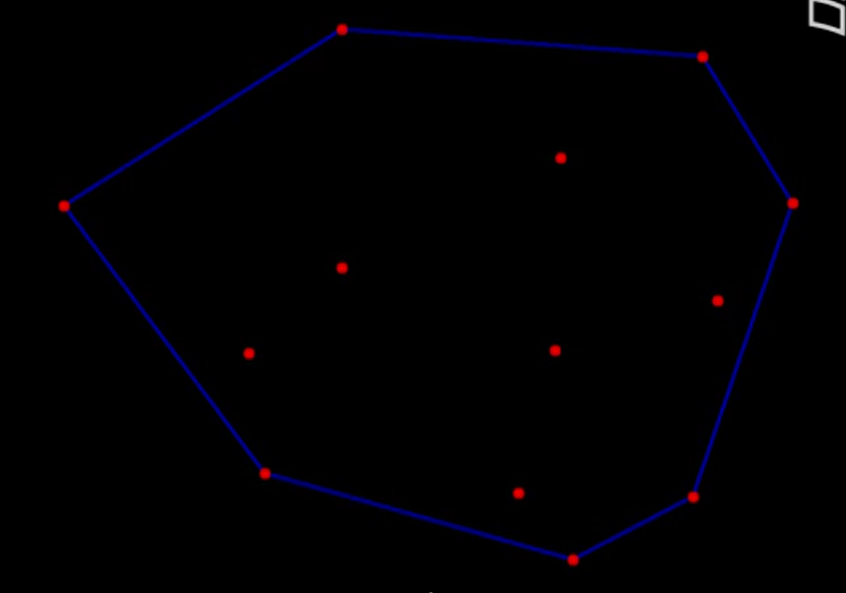
最外面的线段组成的线段集合就成为了凸包，凸包问题便是一系列关于凸包的长度面积求解的算法。

那我们从简单的二维角度去讨论当前的问题,类比高等数学中的仿射变换，我们如下定义Convex Combination

给定一个点集S，S中点属于欧氏空间，令向量λ为n个不同λ组成的列向量，并且满足Σλi =1、n个λ均大于零

则有Σλi*Pi 称为S的凸包

2)极点

我们在图中可以看出，若某点是凸包上面的点，那么一定存在某条直线，使得所有的点（除了这个点）均在直线同侧

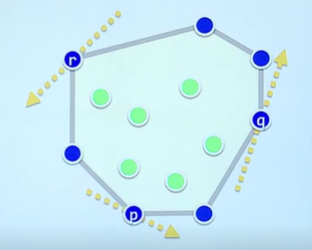
 则我们如下定义极点:

 给定的凸包集合，其中的点就成为极点

 那么我们如何鉴别极点和非极点呢，显然有如下法则：

极点一定不在图中如何三角形中，反过来说，如果某点不是极点，则一定能在图找到一个三角形，使其在三角形内部

显然问题现在转化只需要枚举所有的三角形和点并且实现judge函数判断即可。

时间复杂度：O(n^4)

那么如何实现insideTriangle函数？

我们考虑实现这样的一个事情，我们观察到如果一个点在三角形内部，那么对于三角形三边，若定义逆时针为方向，那么点跟三个有向边一定在同侧

即要么都在线段左侧，要么都在线段右侧（右侧情况由于选择顺时针为方向）。

则经过上述讨论，我们只需要实现一个判断  Toleft  函数，让三次测试结果完全相同即可，下面问题转化成如何实现 Toleft  函数

实现  Toleft  函数

 观察上述图，考虑海伦面积公式公式，不难导出这样上述面积是有方向的，那么我们可以判断行列式正负来判断是左侧还是右侧

接下来展示行列式组成

 利用行列式来记忆是十分有助于对问题进行解释并且在编程过程中能更清楚的实现函数功能

主体实现如下：

bool Toleft(Point a,Point b,Point c){
    return area2(a,b,c)>0;
}
int area2(Point a,Point b,Point c){
    return a.x*b.y+b.x*c.y+c.x*a.y
    -a.y*b.x-b.y*c.x-c.y*a.y;
}

3）极边

从上述求解过程中，我们可以明显看出来代码复杂度还是太高了，既然点可以作为判断的依据，那么我们考虑边的情况，我么有如下定义：

凸包中的边就是极边

那么我们可以经过观察得到，极边的充要条件是所有点都在同一侧，不存在有点分居在线段两侧。

我们可以以此枚举每条边，并且对这个边和所有点进行判断，如果能够判定情况，那么便可以进行判定这个边是凸包中的极边

算法复杂度是：O（N^3）

相较于枚举点的请款，对于极边的情况进行处理，有着更好复杂度

4）Jarvis March 算法

引入

我们考虑选择排序算法的情况，如图所示：

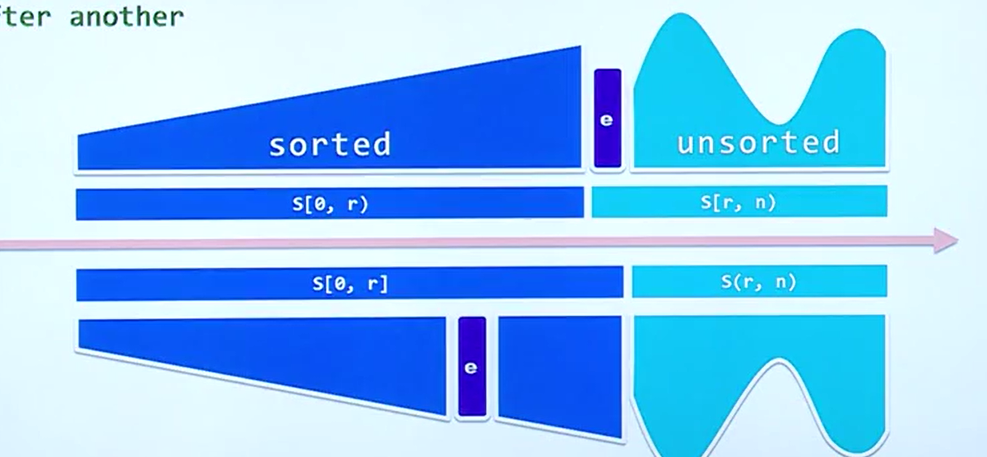
 整个思想来自于，对于未排序的部分我们抽出一个未排序的点，并且在排序完成部分找到对应的位置插入并且将其后的所有点向后移动直到队尾。

那么凸包就像是这样的一个情况，对于未加入的点，我们考虑说是否能利用选择排序的思想完成插入的过程

但是很不幸是由于插入之后的移动的复杂度是O（n）并且sorted部分是动态的无法基于简单的线性结构利用Binary Search来实现O(log n)查找

所以这个算法是实现是有问题的

但是这并不意味着这个思想是无意义的，相反我们发现我们可以通过借用排序算法的思想来实现对凸包算法的情况的实现和拓展

支撑线

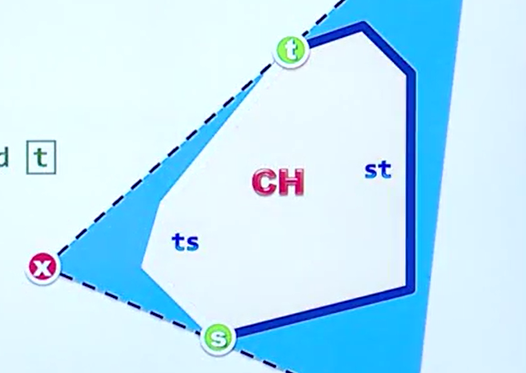
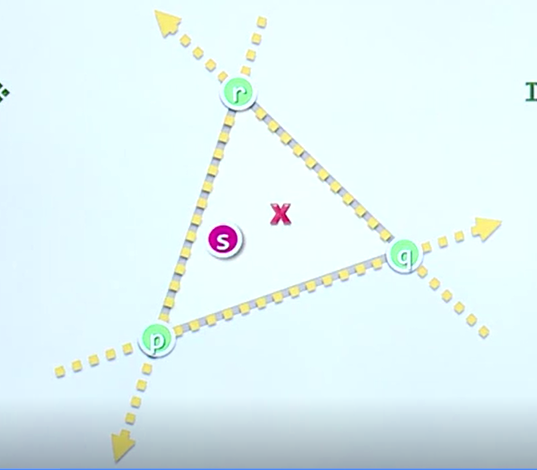
 进一步观察，如图所致，对于新加入进来的点 X 我们对于原凸包做连线，斜率最大和最小的两条线便称为凸包切线，也称支撑线，并且线段另一边一定是凸包上的极点

沿着凸包上面的点向相邻两个点作有向线段，我们可以惊奇的发现，对于点x做函数  Toleft  测试 有如下结果

沿着逆时针方向：

ts 部分：L R

st部分：R L

S点：L L

T点：R R

那么我们就可以在遍历过程中判断点是在ts段还是在st段

进而实现对于凸包的遍历，并且我们可以发现在这个过程中同样可以实现对于点是否在凸包中的检测

再次看选择排序算法

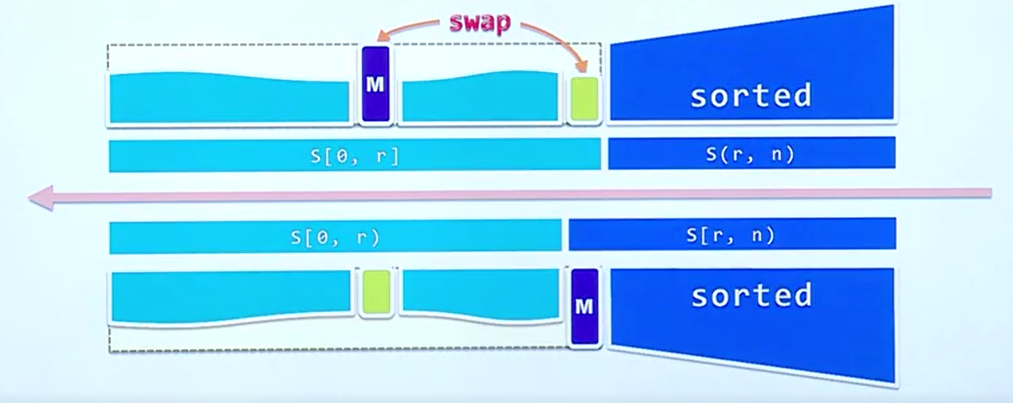
排序算法的基本思想是在于想要在未排序的部分中拿到优先级最高的点（优先级可以是最大、最小、位置最好、斜率最大等等情况），那么在凸包中我们发现对于当前已经有的凸包中的有向线段，有向线段远端的那个点作为基准点，想要选取下一个点的时候只需要选取基准点到目标点的有向线段同上述凸包线段中角度最小的点即可。

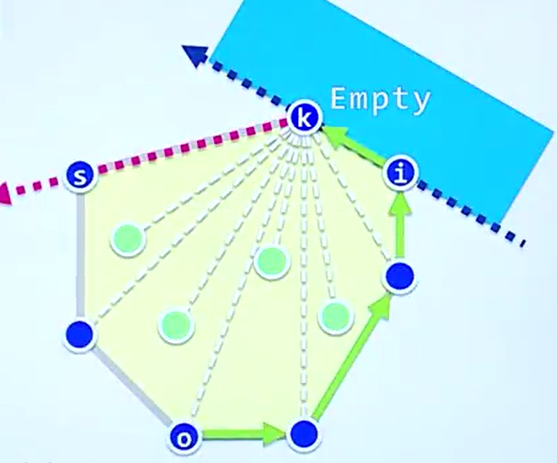
 如何选择角度最小有向线段中的点

显然我们不想借助复杂的三角函数计算来完成这样的判断，那么我们考虑继续结合 Toleft 测试完成这样的目的，比如说我们现在已经选取了某个点作为目标点，记作X，基准点记作K，那么对于遍历得到的下一点S，只需要判断S是否在有向线段 KX 的左边即可，如果在左边，直接进行替换将S赋值到X点。

如何选择最开始的基准点

对于最开始的情况，我们可以有这样的猜想，图中必定有y坐标最小的点，那么我们是不是可以遍历所有点，将y坐标最小的点找到

那么这个点一定是凸包中的极点，显然可证。

但是如果出现多个y值相同的最小点呢

那我们对于这样的歧义，只需要选择最左边的点即可

 5）lower bound

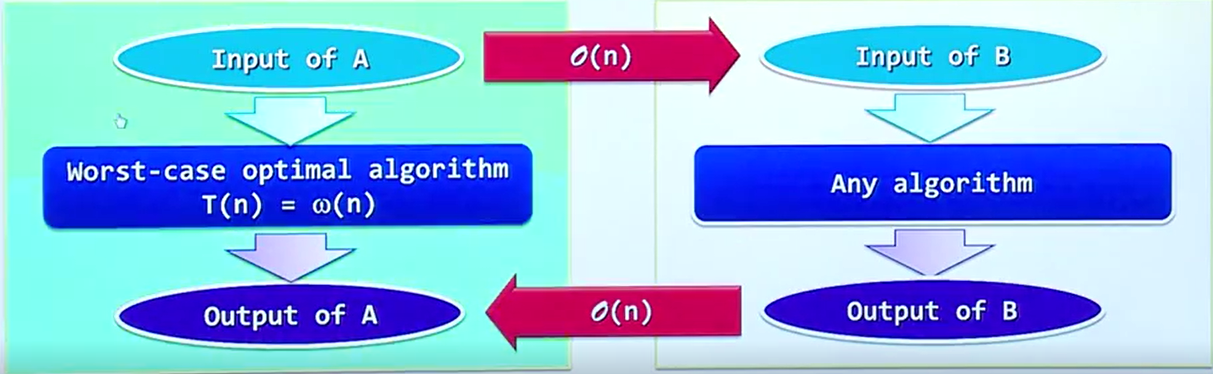
对于一个一个复杂的问题，我们一般情况下是很难直接对问题的复杂度下限进行一个合理的评估的，所以我们渴望能够通过间接的方法来完成对于问题的进一步确定

这里我们引入规约这样的定义来更加详细的解决这样的问题

　　对于A问题的任何一个输入，如果能够在线性时间内，转换成B问题的输入，并且无论B问题其中算法的是什么样子的，只要B问题的输出能够在线性时间内转换成A问题的输出，那么我们就可以认为二者具有着规约关系，即A问题的时间复杂度的下界一定是跟B问题的时间复杂度的下界相同，如此这样的情况可以认为是规约。

　　那么我们看二维凸包问题和经典的一维排序问题之间是否存在明显的规约关系呢，答案是肯定的。

　　我们假定有这样一个函数  y=f(x)  ，那么不难得到，任何一个无序的集合中的点都可以在线性时间内通过函数来映射到二维空间中去，那么我们经过了一个算法，得到了凸包，任何一个在凸包中的点都可以在线性时间内通过反函数映射回 X 轴，并且不难发现，映射回的值一定是在X轴上面单调有序的，这样我们就可以发现确实排序算法和凸包算法可以规约，称为 A is reducial to B A问题可以规约到B 同样也可以记作 A <= B，其中的情况如下图所示。

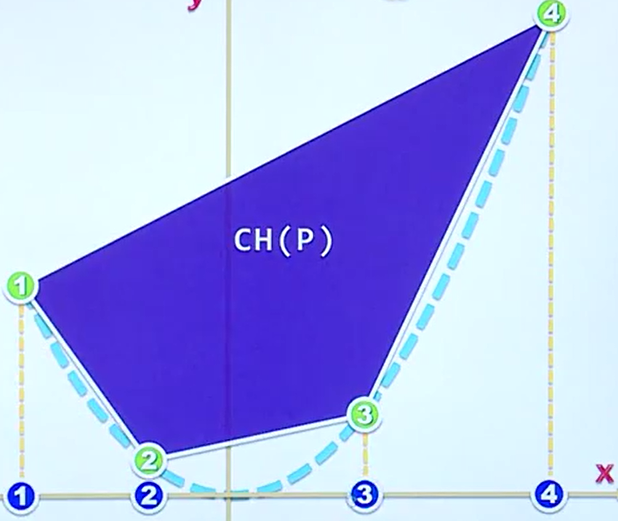
我们已经可以通过一定的证明，知道在一般的情况下，排序算法的复杂度是 O(n log n) 那么显然，凸包算法的复杂度的复杂度下界一定是 O(n log n)

 6) Graham Scan 算法

　　通过上面的分析我们发现，现在的算法复杂度下限已经减小到O(n log n)这样的复杂度，我们所需要做的就是渴望找到这样一个算法能够实现我们想要的东西，我们不妨先看一看这样一个扫描线算法，先理解其大体过程，之后再考虑是否能够证明其复杂度以及正确性的情况。

　　具体过程如下：

1.我们得到一个已知的极点，并且将所有点同这个点进行极角排序

2.选取角度最低的点连成一条边，显然这条边就是极边，并且将这两个点压入栈S中

3.依次将剩余点按照次序压入T中（这个次序是排序的倒序，因为是栈，栈顶元素是原来排序第二的点，其余的以此类推）

4.拿到T的栈顶元素T[0]，并且取出S栈的栈顶两个元素S[0],s[1],并且组成有向边 (S[1]S[0])

5.如果T[0]在有向边的左边，则压入S栈中

6.否则，将S的栈顶元素弹出（意味着回退这样的一条边）直到能满足（5）中情况

7.最后当T中没有元素，将S栈中的元素弹出，并且存储在数组中，这个数组中的元素就是整个凸包中的元素并且是按照顺时针顺序排列

如下图所示是我们的一个例子的最终情况：

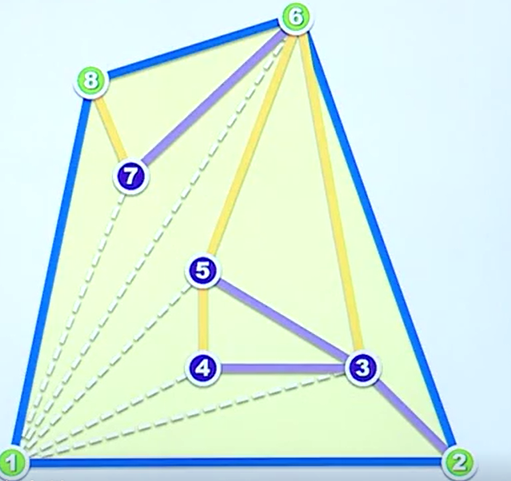
从图中我们不难看出上述过程中的得到的结果是最终正确，那么整个算法的正确性如何证明的？

不妨使用归纳假设法，假设判断到K个点都成立，现在要加入第K+1个点，那么无非两种情况，在原来的右边或者原来的左边，如果左边，则加入点，显然满足凸包的定义

但是如果是右边，则我们回溯直到能满足这样一个点在凸包的情况（可能在边上也可能在内部）

综上所述，我们在算法进行过程中，始终能保证凸包的性质是完全满足的，如此说明，上述算法的正确性是得到保证的。

接下来我们考虑复杂度的情况：

因为有些边可能发生回溯的情况，如果每一个点都发生回溯的情况，并且能回溯到最初始的边，我们是否能够认为，复杂度是O(n^2)呢

由欧拉公式我们发现，其实上述算法中产生的图是平面图，即不会在图面上面发生线条的重叠，那么欧拉曾经证明过，这样的线的条数是O(3n)的，这样的话限制我们算法的复杂度最多只能到达O(n)的级别

那么有没有可能S栈中元素全部被弹出呢，显然由于初始情况下我们选择就是一个极边，所以所有点都在此有向线段的左边，故而能够保证算法的完成度。

拓展情况

如果说我们得到的序列元素已经是在一个维度上面有序呢？是不是需要还是按照上面我们所叙述的那样进行操作嗯？好消息是不必这样，我们可以假想在无穷远处有两个点（正负无穷各一个），那么所有线段可以近似看成平行的，那么极角排序的情况就自然而然认为是X的大小进行排序。

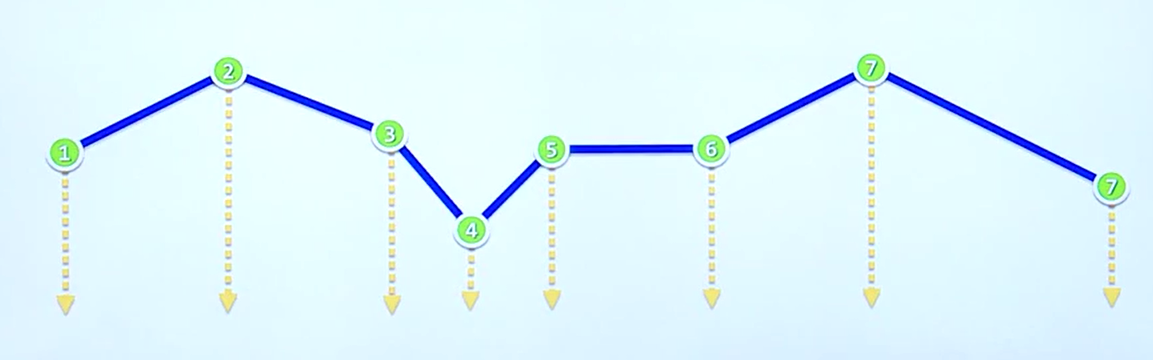
 这样的话，我们可以直接对上凸包元素进行排序，同理再对下凸包进行排序，这样我们就可以完成整个凸包的计算。

 

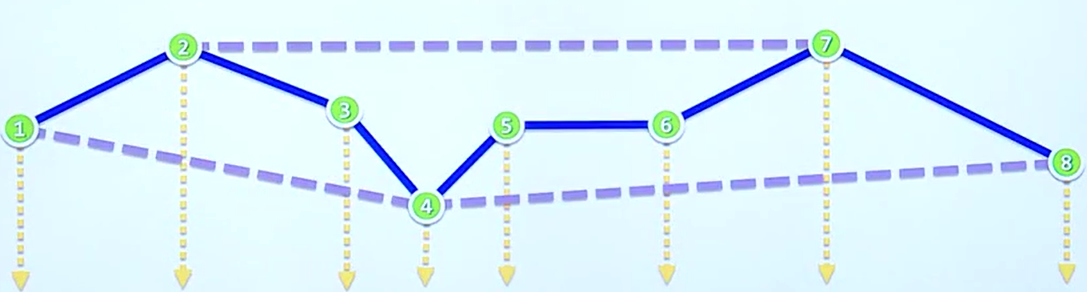
我们将根据上述所述的Scan算法给出答案，详见最后的代码

 7）分治算法

如果我们按照排序的思想更深一步进行思考，是否能在归并排序的基础上完成凸包算法的设计呢，答案是显然的。如果我们按照X为准进行排序

那么显然，我们可以得到一个个相互不重叠的子凸包，这样的话我们需要解决的问题就是如何对两个子凸包进行合并，观察我们下图，是否有想法呢？

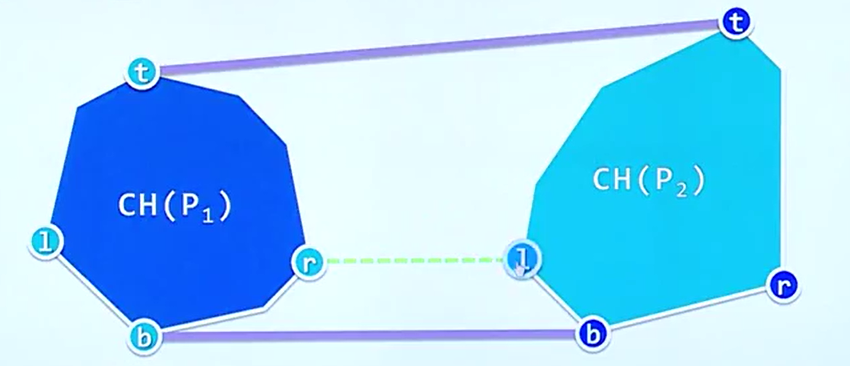
 直觉告诉我们，我们只需要找到凸包中的最高点即可，并且做两个凸包的公切线，答案不就出来了吗，那么我们再看看下面的图，真的是这么简单吗？

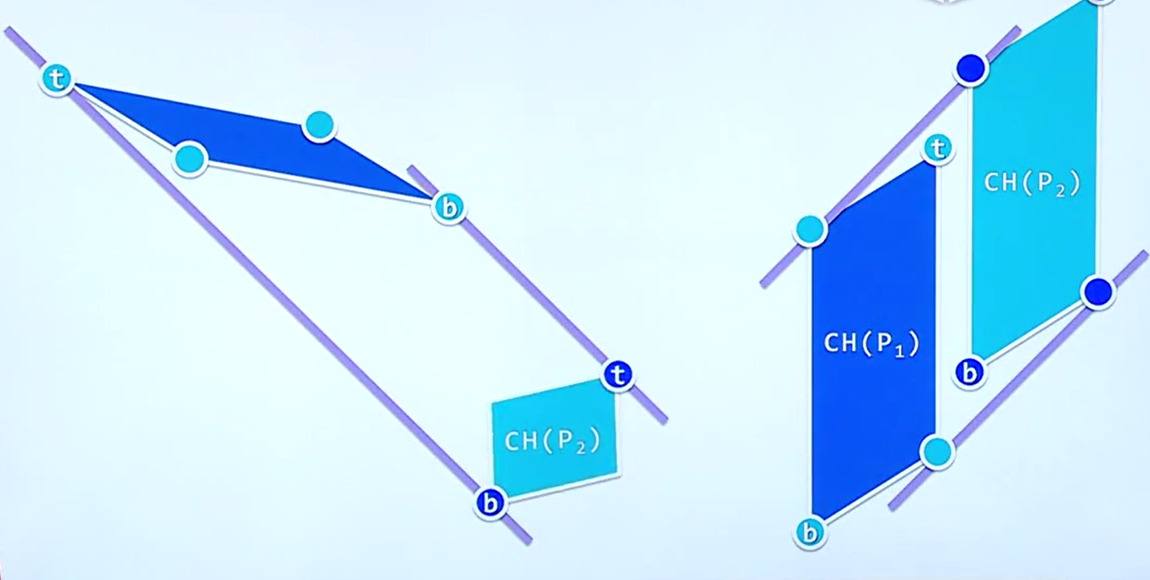
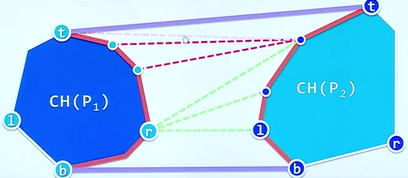
显然，我们直觉出现了问题，这样的话，我们考虑我们之前已经学过的一个图我们无非是想去做另一个凸包的切线（又称支撑线），而相较于另一个凸包，也只是做这个凸包的切线，而切点的时候，所有toLeft函数测试结果是同号的

我们只需要不断向上或者向下去测试这样一条线段的端点的前驱和后继是否是toLeft测试结果相同，并且不断向上或者向下Z字形走即可。如图所示，当我们找到两个子凸包的共切点的时候自然而然的明白只需要

将其中包含在合并后的凸包中的点从原来子凸包中剔除出去即可，这样我们就完成了对于子凸包的合并

8）代码实现

 凸包的例题：题面

完整代码实现如下:记得toLeft函数记得开long long（因为这个错了两次调了好久）

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+7;
const int INF=0x7f7f7f;
#define LL long long
class Point{
public:
    LL x,y;
    int index;
};
Point s[N];

bool cmp(Point a,Point b){
    return a.x<b.x;
}

bool toLeft(Point a,Point b,Point c){//用于判断ab有向线段，c是在线段左边还是右边
    LL ret=a.x*b.y-a.y*b.x+
            b.x*c.y-b.y*c.x+
            c.x*a.y-c.y*a.x;
    return ret>=0;
}
int find_lowest_leftest(Point s[],int n){//找到最低最左的点
    int pos=0;
    for (int i=1;i<n;i++){
        if (s[i].y<s[pos].y){
            pos=i;
        }
        if (s[i].x<s[pos].x&&s[i].y==s[pos].y){
            pos=i;
        }
    }
    return pos;
}

void sort(int L,int R,Point s[]){//找到起始边
    if (R==L) return;
    int mid=(L+R)>>1;
    sort(L,mid,s);
    sort(mid+1,R,s);
    int pos1=L,pos2=mid+1;
    vector<Point> v;
    while (pos1<=mid&&pos2<=R){
        if (toLeft(s[0],s[pos1],s[pos2])){
            v.push_back(s[pos1]);
            pos1+=1;
        }
        else{
            v.push_back(s[pos2]);
            pos2+=1;
        }
    }
    while (pos1<=mid){
        v.push_back(s[pos1]);
        pos1+=1;
    }
    while (pos2<=R){
        v.push_back(s[pos2]);
        pos2+=1;
    }
    for (int i=0;i<R-L+1;i++)
        s[L+i]=v[i];
}
int solve(Point s[],int n){//主体算法设计
    stack<Point> S,T;
    S.push(s[0]);
    S.push(s[1]);
    for (int i=n-1;i>1;i--)
        T.push(s[i]);
    while (!T.empty()){
        Point tmp=T.top();T.pop();
        bool flag=true;
        while (flag){
            Point P1=S.top();S.pop();
            Point P2=S.top();S.pop();
            if (toLeft(P2,P1,tmp)){
                flag=false;
                S.push(P2);S.push(P1);S.push(tmp);
            }
            else{
                S.push(P2);
            }
        }
    }
    int tot=0;
    int a[N];
    while (!S.empty()){
        Point tmp=S.top();S.pop();
        a[tot++]=tmp.index;
    }
    long long ans=1;
    for (int i=0;i<tot;i++)
        ans=(ans*1LL*a[i])%(n+1);
    ans=(ans*tot)%(n+1);
    return (int)ans;
    
}
int main(){
    int n;scanf("%d",&n);
    for (int i=0;i<n;i++){
        int x,y;scanf("%d%d",&x,&y);
        s[i].x=x;s[i].y=y;s[i].index=i+1;
    }
    int pos1=find_lowest_leftest(s,n);
    swap(s[pos1],s[0]);
    sort(1,n-1,s);
    int ans=solve(s,n);
    printf("%d\n",ans);
    return 0;

// 注意在运算过程中，是否发生了爆int的情况