SVM个人学习总结
如题,本文是对SVM学习总结,主要目的是梳理SVM推导过程,以及记录一些个人理解。
1.主要参考资料
[1]Corres C. Support vector networks[J]. Machine Learning, 1995, 20(3):273-297.
[2]Platt J C. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines[C]// Advances in Kernel Methods-support Vector Learning. 1998:págs. 212-223.
[3]结构之法 算法之道:支持向量机通俗导论(理解SVM的三层境界)
[4]Free Mind:支持向量机系列
[5]JerryLead:支持向量机系列
[6]周志华: 《机器学习》
[7]zouxy09的专栏:机器学习算法与Python实践之(四)支持向量机(SVM)实现
[8]Jasper:SVM入门(一)至(三)Refresh
[9]Xianling Mao的专栏:深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
(以上参考资料可能是本篇博客价值最大的地方了)
2.推导思路简析
1.线性可分基本模型(几何问题,凸优化问题,不等式约束)
2.对偶问题:拉格朗日乘子法,KKT条件
3.SMO算法:求解对偶问题
4.软间隔:引入松弛变量和惩罚函数
5.线性不可分:高维映射与核函数
3.1 线性可分基本模型
(1)问题描述:对于给定的两类训练样本,找到一个超平面将其分成两类。
在样本空间中,超平面可以用如下线性方程描述:$$w^T x + b = 0 ag{3.1.1} $$
**SVM的目的:寻找最优的超平面(w,b)。 **
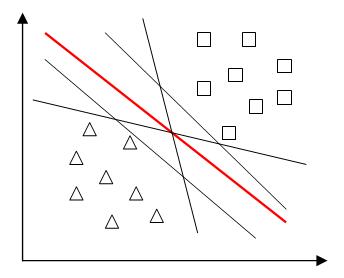
(2)如果仅仅是为了把两类训练样本分开,可以有多个超平面将其分开,但是我们追求最好的超平面,以便在预测时有更强的泛化能力。从直观上看,当两类样本点均远离超平面时,超平面分类效果更好,即所有样本点到超平面的最小距离越大,超平面分类效果越好。
样本点到超平面的距离可分为函数距离和几何距离。
函数距离: $$r_f = y * (w^T x + b) = yf(x) ag{3.1.2}$$
几何距离: $$r_g = frac{y * (w^T x + b)}{||w||} =frac{ yf(x)}{||w||} ag{3.1.3}$$
由于y的取值是1或-1,并且与f(x)同号,所以函数间隔实际上是|f(x)|,其缺陷是当w和b成比例变化时,超平面不变,但是函数距离会变化,因此不便于统一评价。
几何距离是直观上点到超平面的距离,仅与超平面本身有关,更适合做超平面的评价指标。
任意样本点x到超平面(w^T x + b = 0)的距离: $$ d = frac{|w^T x + b|}{||w||} ag{3.1.4}$$

|
样本点到超平面距离几何公式推导:
设超平面方程为(w^T x + b = 0) ,则w为超平面的法向量;样本点A(x)到超平面的距离为d,B(X0)为A在超平面上的投影。 [vec{BA} = x - x_0 = d*frac{w}{||w||} ag{3.1.6}
] 将(3.1.6)代入(3.1.5), [w^T (x - d*frac{w}{||w||})+ b = 0 ag{3.1.7}
] 化简可得, [d = frac{|w^T x + b|}{|frac{w^Tw}{||w||}|} = frac{|w^T x + b|}{||w||} ag{3.1.8}
] 证毕。 |
(3)假设超平面(w,b)能够将样本正确分类,即对于任意训练样本$(x_i,y_i),y_iin(-1,+1) $,有
则距离超平面最近的几个点,使(3.1.9)式中等号成立,这些点被称为“支持向量”(support vector),
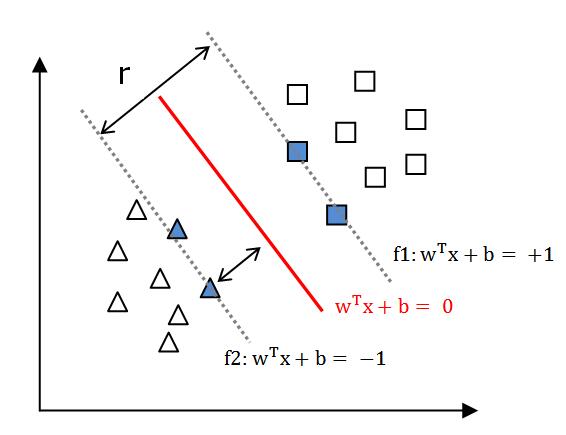
由式(3.1.4)和式(3.1.9)可知,$$ r = frac{2}{||w||} ag{3.1.10} $$
r被称为“间隔”(margin)。显然,当r越大时,超平面(w,b)的分类效果越好。
因此,寻找最优超平面等价于确定w,b,使得r最大,即
为了便于计算,将式(3.1.11)简化为
通过求解式(3.1.12)即可得到最大间隔超平面(w,b):
将新的样本点代入f(x)计算,利用Logistic(f(x))函数进行类别判断正负类。
下面讨论如何求解w,b。
3.2 对偶问题:拉格朗日乘子法,KKT条件
(1)式(3.1.12)是一个包含不等式约束的凸优化问题,利用拉格朗日乘子法,并结合KKT条件,将其转化成“对偶问题”。
对式(3.1.12)的约束条件添加拉格朗日乘子$alpha_i geq 0 $,则该问题的拉格朗日函数为:
令(L(w,b,alpha))对w和b求偏导,置零,得,
将式(3.2.2)代入(3,2,1),消去w,b,并添加KKT约束条件,可得式(3.1.12)的对偶问题,
|
推导过程如下: [L(w,b,alpha) = frac{1}{2}||w||^2 + sum_i^m alpha_i(1-(y_i(w^T x_i + b))) \
=frac{1}{2}w^Tw-sum_i^malpha_iy_iw^Tx_i -sum_i^malpha_iy_ib + sum_i^malpha_i\
=frac{1}{2}w^Tsum_i^malpha_iy_ix_i - w^Tsum_i^malpha_iy_ix_i -sum_i^malpha_iy_ib + sum_i^malpha_i\
=-frac{1}{2}w^Tsum_i^malpha_iy_ix_i - bsum_i^malpha_iy_i + sum_i^malpha_i\
=sum_i^malpha_i - frac{1}{2}(sum_i^malpha_iy_ix_i)^Tsum_i^malpha_iy_ix_i \
=sum_i^malpha_i - frac{1}{2}sum_i^malpha_iy_ix_i^Tsum_i^malpha_iy_ix_i \
=sum_i^m alpha_i - frac{1}{2} sum_i^m sum_j^m alpha_ialpha_j y_i y_j x_i^T x_j ag{3.2.4}
] |
由(3.2.3)解出(alpha)后,即可求出w,b。
分析约束条件 (alpha _i(y_i(w^T x_i + b)-1) = 0),对任意训练样本((x_i,y_i)),总有(alpha _i = 0)或者((y_i(w^T x_i + b)-1) = 0)。当(alpha_i = 0)时,由式(3.2.2),对应的样本不影响f(x);当(alpha _i eq 0)时,必定有$ (y_i(w^T x_i + b)-1) = 0$,此时样本点在最大间隔边界线上,即该点为支持向量。因此,SVM训练完成后,最终模型仅与支持向量有关。
(2)拉格朗日乘子法与KKT条件的个人理解:(参考文献[6],[9])
**
要求拉格朗日函数对原变量和拉格朗日乘子求偏导并且置零;
拉格朗日函数对原变量求偏导置零——保证目标函数梯度与等式约束条件梯度共向;
拉格朗日函数对拉格朗日乘子求偏导置零——保证等式约束条件成立。
**
**
当凸优化问题问题中包含不等式约束时,拉格朗日乘子法需要结合KKT条件。
KKT条件保证了对偶函数是原问题的解的下界,并且不论原问题的凸性如何,对偶问题始终为凸优化问题。
当满足一定条件时,即“强对偶性”,对偶问题的最优解就是主问题的最优下界。
KKT条件意义:是一个非线性规划(Nonlinear Programming)问题有最优解的充分必要条件。
**
3.3 SMO算法:求解对偶问题
(1)分析对偶问题(3.2.3),目标函数中仅有变量(alpha),求解出(alpha)即可解决所有问题。SMO算法是目前解决这个问题的最高效算法。
SMO的基本思路:
“任意”设定一组(alpha_i),即设定所有待求参数的初始值;
选取一对需要更新的变量(alpha_i) 和(alpha_j);
固定(alpha_i) 和(alpha_j)之外的参数,求解式(3.2.3),更新选取的变量(alpha_i) 和(alpha_j);
重复以上两个步骤直到满足停止迭代的条件。
(2)ai的选取原则:SMO首先选呢去违背KKT条件程度最大的变量,变量更新后可能导致目标函数减幅最大;
aj的选取原则:启发式选取,使选取的两个变量所对应的样本之间的间隔最大。
SMO算法高效的原因:每次仅计算两个参数的过程非常高效,并且两个参数满足等式约束条件,即每次实际上只用计算一个参数(这也是为什么每次需要选取两个参数的原因),所求问题转化成一元二次函数极值问题(抛物线)。
(3)求解出(alpha)后,利用式(3.2.2),可求解出w;
确定偏移项b时,常用所有支持向量求解的平均值:$$b = frac{1}{|S|} sum_s(y_s sum_ialpha_i y_j x_i^T x_s) ag{3.3.1}$$
其中S为所有支持向量的下标。
至此,w,b已经求解完成,SVM的初步推导结束。
3.4软间隔:引入松弛变量和惩罚函数
(1)在具体任务中,样本并不能理想地完全分开,或者生硬的分离两类样本后模型泛化能力很差。如下图所示,有两个样本点偏离,若按照原先的分离规则,求出的超平面为图中红色虚线所示,显然这并不是理想的结果。因此,为了避免过拟合,我们允许某些样本点不满足约束条件(如图中红色样本点),并引入了“软间隔”。
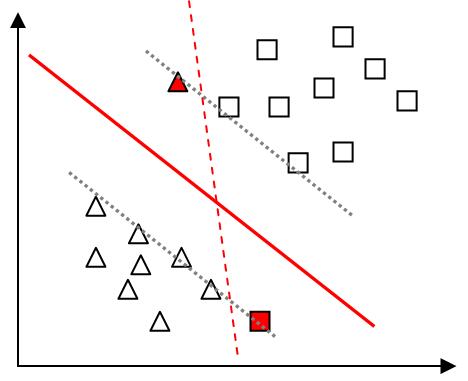
(2)正则化:引入软间隔后,放宽约束条件$ y_i(w^T x_i + b) geq +1$,引入松弛变量后,有
对应的拉格朗日函数变为
令(L(w,b,alpha,xi,mu))对(w,b,xi_i) 求偏导并置零,将其代入上式整理得到对偶问题,
对比(3.2.3)分析可知,引入软间隔后仅仅影响对偶变量(alpha_i)的约束条件,不改变目标函数。
因此,引入软间隔后,只需要在用SMO求解(alpha_i)时注意约束条件,其他求解步骤与硬间隔相同。
3.5线性不可分:高维映射与核函数
(1)SVM最大的优点就是可以高效解决线性不可分的分类问题,使用的方法是函数映射。
对于线性不可分问题,把原始空间映射到更高维空间,使其线性可分,(已有定理证明:当样本空间是有限维空间,则一定存在高维特征空间使其样本可分)。
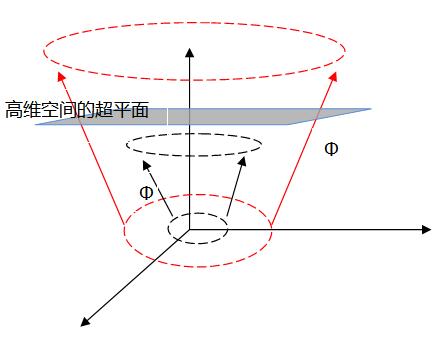
令(Phi(x))表示映射后的特征向量,则映射的超平面模型为, $$f(x) = w^T Phi(x) + b ag{3.5.1}$$
其主问题变为,$$max_(w,b)frac{2}{||w||}
s.t. y_i(w^T Phi(x_i)+ b) geq +1 , i = 1,2,cdots,m. ag{3.5.2} $$
相应地,对偶问题变为,
(2)在高维空间计算向量内积时(Phi(x_i)^T Phi(x_j)),可能产生维数灾难,计算十分困难。为了解决这个问题,引入了核函数。假设函数:
则只用在原始低维样本空间中计算函数(k(x_i,x_j))的结果,等价于高维空间计算向量内积(Phi(x_i)^T Phi(x_j)),从而得以避免维数灾难。
这样的函数(k(x_i,x_j))称为核函数。
例如:
利用核函数替代(Phi(x_i)^T Phi(x_j)),则对偶问题变成,
通过SMO算法,可求解出(alpha),进一步得到,
(3)由以上分析,只需构造一个合适的核函数,即可代替计算映射内积(Phi(x_i)^T Phi(x_j)),完全不用理会映射(Phi(x))的具体形式,非常奇妙。
另外,Mercer定理指出,一个对称函数所对应的核矩阵半正定,则其可作为核函数使用。Mercer定理完美解决了核函数的构造问题。
超平面方程是以支持向量为参数的非线性函数的线性组合,仅与支持向量的数量有关,独立与空间的维度,因此保证了SVM能有效处理高维数据。
常用的核函数有线性核,多项式核,高斯核,拉普拉斯核,Sigmoid核。
4.总结
(1)SVM是基于统计学习理论的一种机器学习方法,通过寻求结构风险最小来提高泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本较少的情况下,也能获得良好的统计规律目的。
(2)SVM是一种二分类模型,基本定义是特征空间上的间隔最大的线性分类器,学习策略是间隔最大化,最终转换成一个凸二次优化规划问题的求解,利用SMO算法可高效求解该问题。
(3)针对线性不可分问题,利用函数映射将原始样本空间映射到高维空间,使得样本线性可分,进而SMO算法求解通过拉普拉斯对偶问题。在计算高维空间的内积时,利用核函数巧妙转换,利用原始样本空间计算结果代替高维空间的内积计算。Mercer定理明确了核函数的构造方法。
(4)遗留问题:对偶问题和KTT条件还未理解透彻;核方法——针对特定问题核函数的选取与构造;SVM多分类;支持向量回归SVR。