欧拉函数

概念

欧拉函数，φ(N)，表示小于等于n并与n互质的数的个数.

怎么求欧拉函数

1.显然，当N为质数，φ(N)=N-1

2.用(1)的特殊情况求出其他φ(N)，枚举质数j,求出φ(i*j).

若i mod j=0，那么i包含了i*j的所有质因子，所以φ(i*j)=φ(i)*j.

否则，我们可以知道gcd(i,j)=1,所以φ(i*j)=φ(i)*φ(j).

    phi[1]=1;
    for(int i=2;i<=1000000;i++)
    {
        if(flag[i]==0)
        {
            p[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt;j++)
        {
            if(i*p[j]>1000000)
            {
                break;
            }
            flag[i*p[j]]=1;
            if(i%p[j]==0)
            {
                phi[i*p[j]]=p[j]*phi[i];
                break;
            }
            else
            {
                phi[i*p[j]]=(p[j]-1)*phi[i];////由于p[j]为质数，所以(p[j]-1)=phi[j]
            }
        }
    }    

一道题（非模板）

题面

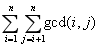
1349. 最大公约数 (Standard IO)
Time Limits: 1000 ms  Memory Limits: 65536 KB  

Description
　　小菜的妹妹小诗就要读小学了！正所谓计算机要从娃娃抓起，小菜决定在幼儿园最后一段轻松的时间里教妹妹编程。
　　小菜刚教完gcd即最大公约数以后，一知半解的妹妹写了如下一段代码：
　　 sum:=0;
　　 for i:=1 to n-1 do
　　 for j:=i+1 to n do sum:=sum+gcd(i,j)

　　显然这个程序的效率是很低的，小明打算写一个更强的程序，在求出sum的同时比妹妹跑的更快。

Input
　　第一行一个整数t，即表示有t组数据
　　接下来t行，每行一个整数n

Output
　　t行，每行一个整数，表示n所对应的sum值

Sample Input
2
10
100

Sample Output
67
13015

Data Constraint

Hint
【数据规模】
　　20%数据t≤100,n≤100
　　40%数据t≤1000,n≤2000
　　100%数据t≤10000,n≤1000000

思路

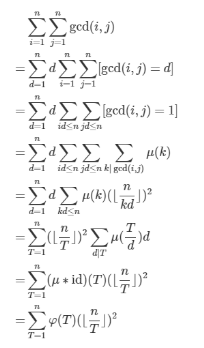
 code

#include<bits/stdc++.h>
#define inf 1000000007
using namespace std;
int n,m,t,phi[1000005],flag[1000005],p[1000005],cnt;
long long sum[1000005];
int main ()
{
    //freopen(".in","r",stdin);
    //freopen(".out","w",stdout);
    phi[1]=1;
    for(int i=2;i<=1000000;i++)
    {
        if(flag[i]==0)
        {
            p[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt;j++)
        {
            if(i*p[j]>1000000)
            {
                break;
            }
            flag[i*p[j]]=1;
            if(i%p[j]==0)
            {
                phi[i*p[j]]=p[j]*phi[i];
                break;
            }
            else
            {
                phi[i*p[j]]=(p[j]-1)*phi[i];
            }
        }
    }
    for(int i=1;i<=1000000;i++)sum[i]=sum[i-1]+phi[i];
    for(scanf("%d",&t);t--;)
    {
        scanf("%d",&n);
        long long ans=0;
        for(int l=1,r,x;l<=n;l=r+1)
        {
            x=n/l;r=n/x;
            ans+=1ll*(x)*(x)*(sum[r]-sum[l-1]);
        }
        ans=(ans-1ll*(n+1)*n/2)/2;
        printf("%lld\n",ans);
    }
    return 0;
}