双向链表
上文中详解了单向链表, 本节主要针对双向链表的原理、优缺点以及各个操作进行讲解。
双向链表对于单项链表来说,它支持两个方向,每个结点不止有一个后继指针next指向后面的结点,而且还有一个前驱指针prev指向前面的结点,结合图来看看:

从图中可以看出,双向链表需要额外的两个空间来存储后继结点和前驱节点的地址。所以存储同样的数据,双向链表要比单向链表占用更多的空间。虽然说两个指针比较浪费空间,但是可以支持双向遍历,这样也带来了双向链表操作的灵活性。总结一下双向链表的优缺点:
优点:
- 对于链表中给定的一个结点,可以从两个方向进行操作。但是,在单向链表中,只有获取结点的前驱节点的指针,才能后删除该节点。
- 在双向链表中,每个结点都有一个指向前驱结点的指针,可以直接后退到前驱结点。
缺点:
- 每个结点需要再添加一个额外的指针,因此需要更多的空间开销
- 结点的插入和删除更加的费时(需要更多的指针操作)
双向链表的操作:
首先,我们先初始化一个双向链表:
package com.xb.other; /** * Author Mr. Guo * Create 2019/8/11 - 12:22 */ public class DLLNode { private int data; private DLLNode next; private DLLNode preivous; public DLLNode(int data) { this.data = data; } public int getData() { return data; } public DLLNode getNext() { return next; } public DLLNode getPreivous() { return preivous; } public void setData(int data) { this.data = data; } public void setNext(DLLNode next) { this.next = next; } public void setPreivous(DLLNode preivous) { this.preivous = preivous; } }
插入:
-
- 在链表的头部插入结点
在这种情况下,在将新结点插入表头结点之前。修改前驱指针和后继指针的值需要两步操作:
- 1、将新结点的后继指针更新为指向当前的表头结点,将新结点的前驱指针赋值为NULL。

2、将原表头结点前驱指针更新为指向新结点,然后将新结点作为表头。

-
- 在链表的末尾插入结点
这种情况下,需要遍历到链表的最后,然后插入新结点。
- 1、新结点的后继指针指向为NULL,前驱指针指向表尾节点。

2、将原表尾节点的后继指针指向新结点。
- 在链表的中间插入结点
这种情况下,需要遍历表知道位置结点,然后插入新结点。
1、新结点的后继指针指向需要插入新结点的位置结点的后继指针。然后令新结点的前驱指针指向位置结点。
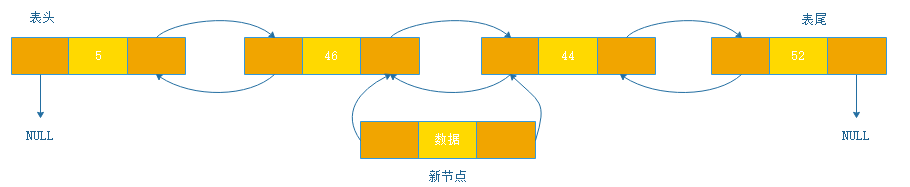
2、位置结点的后继指针指向新结点前驱指针,位置结点的后继结点的前驱指针指向新结点的后继指针
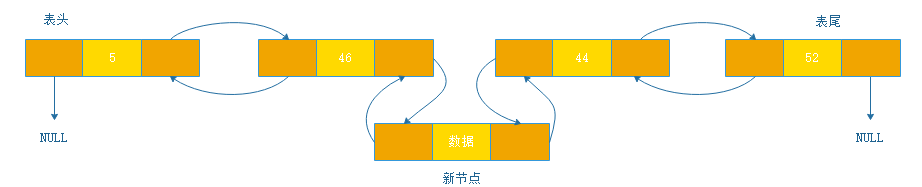
代码实现:
/** * 获取双向链表的长度 */ public int getLength(DLLNode headNode) { int length = 0; DLLNode currentNode = headNode; while (currentNode != null) { length++; currentNode = currentNode.getNext(); } return length; } /** * 链表插入操作 */ public DLLNode DLLInsert(DLLNode headNode, DLLNode nodeToInsert, int position) { // 如果链表为空,则直接插入 if (headNode == null) { return nodeToInsert; } //先获取链表长度 int size = getLength(headNode); // 如果插入位置超出了链表范围,则直接返回头结点,插入范围在[1,size+1] if (position > size + 1 || position < 1) { System.out.println("Posititon of nodeToInsert is invalid." + "The valid inputs are1 to " + (size + 1)); return headNode; } // 如果是在头结点插入 if (position == 1) { nodeToInsert.setNext(headNode); headNode.setPreivous(nodeToInsert); return nodeToInsert; } else { // 如果在链表的中间或尾部插入 DLLNode previousNode = headNode; int count = 1; while (count < position - 1) { previousNode = previousNode.next; count++; } DLLNode currentNode = previousNode.getNext(); nodeToInsert.setNext(currentNode); if (currentNode != null) { currentNode.setPreivous(nodeToInsert); } previousNode.setNext(currentNode); currentNode.setPreivous(previousNode); } return headNode; }
复杂度分析:
时间复杂度为O(n)。在最坏情况下,需要在链表的尾部插入结点。
空间复杂度为O(1)。用于创建临时变量。
删除:
-
- 删除链表的表头结点
这种情况下,需要从双向链表中删除第一个结点,需要通过两步来实现:
1、创建一个临时结点,让它与表头指向同一个结点

2、修改表头结点指针,使其指向下一个结点(headnode=headnode.next),将表头结点的前驱指针更改为NULL(head.setpreivous(NULL)),然后移除临时结点。

-
- 删除链表的表尾结点
该种情况下处理,比删除双向链表的第一个结点要复杂一些,因为要找到尾节点的前驱结点,需要通过三步来实现:
1、遍历链表,在遍历的时候,还要保持前驱(前一次经过的)结点的地址。当遍历到表尾时,有两个指针分别指向表尾结点的tail指针和指向表尾结点的前驱结点指针。

2、更新表尾的前驱结点的next指针为NULL

3、移除表尾结点

-
- 删除链表的中间结点
这种情况下,删除的结点总是位于两个结点之间,因此表头和表尾的值不需要更新。该删除操作可以分为两步来完成:
1、遍历链表,遍历链表的时候保存前驱(前一次经过的)结点。一旦找到要删除的结点。更改前驱结点的next指针使其指向被删除结点的下一个结点,更该被删除结点的后继结点的previous指针指向被删除结点的前驱结点。

2、移除被删除的当前结点

代码实现
/**
* 链表的删除操作
*/
public DLLNode DLLDelete(DLLNode headNode, int position) {
//获取链表的长度
int size = getLength(headNode);
//如果删除的位置不在链表的范围内,则直接返回
if (position > size || position < 1) {
System.out.println("Posititon of node to delete is invalid." + "The valid inputs are1 to " + size);
return headNode;
}
if (position == 1) {
DLLNode currentNode = headNode.getNext();
headNode = null;
currentNode.setPreivous(null);
return currentNode;
} else {
DLLNode previousNode = headNode;
int count = 1;
while (count < position -1) {
previousNode = preivous.next;
count++;
}
//要删除的当前结点
DLLNode currentNode = previousNode.getNext();
DLLNode laterNext = currentNode.getNext();
previousNode.setNext(laterNext);
if (laterNext != null){
//如果被删除的结点不是NULL结点,那么设置其前驱结点指针指向被删除结点的前驱指针
laterNext.setPreivous(previousNode);
currentNode = null;
}
}
return headNode;
}
时间复杂度分析:
时间复杂度为:O(n),在最差的情况下,可能需要删除链表尾部结点
空间复杂度为:O(1),仅用于创建一个临时变量。