缓解过拟合

1.欠拟合与过拟合的解决办法

                                          

 

 

 

 案例：

实现拟合

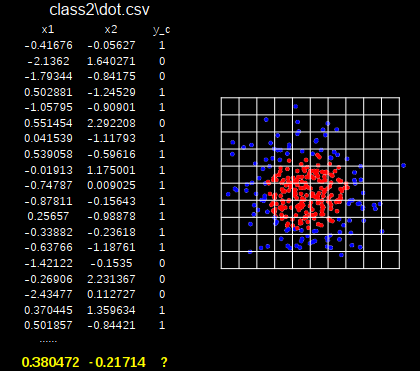
（1）不加入正则化

轮廓不够平滑，存在过拟合

#! /usr/bin/env python
# -*- coding:utf-8 -*-

import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

# 读入数据/标签，生成x_train, y_train
df = pd.read_csv('./datasets/dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])

x_train = np.vstack(x_data).reshape([-1, 2])
y_train = np.vstack(y_data).reshape([-1, 1])

Y_c = [['red' if y else 'blue'] for y in y_train]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)

# from_tensor_slices函数切分传入的张量的第一个维度，生成相应的数据集，使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
print(train_db)

# 生成神经网络的参数，输入层为2个神经元，隐藏层为11个神经元，1层隐藏层，输出层为1个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11], dtype=tf.float32))
b1 = tf.Variable(tf.constant(0.01, shape=[11]))

w2 = tf.Variable(tf.random.normal([11, 1], dtype=tf.float32))
b2 = tf.Variable(tf.constant(0.01, shape=[1]))

# 设置学习率
lr = 0.005
# 设置循环轮数
epochs = 800

# 训练部分
for epoch in range(epochs):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:  # 记录梯度信息
            # 记录神经网络乘加运算
            h1 = tf.matmul(x_train, w1) + b1
            # 经过激活函数reLu
            h1 = tf.nn.relu(h1)
            # 计算输出y
            y = tf.matmul(h1, w2) + b2

            # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss = tf.reduce_mean(tf.square(y_train - y))

        # 计算loss 对各个参数的梯度
        variables = [w1, b1, w2, b2]
        grads = tape.gradient(loss, variables)

        # 实现梯度更新
        # w1 = w1 - lr * w1_grad tape.gradient是自动求导结果与[w1, b1, w2, b2] 索引为0，1，2，3
        w1.assign_sub(lr*grads[0])
        b1.assign_sub(lr*grads[1])
        w2.assign_sub(lr*grads[2])
        b2.assign_sub(lr*grads[3])

    # 每20个epoch，打印loss
    if epoch % 20 == 0:
        print('epoch:', epoch, 'loss:', float(loss))

##################### 预测 ##############################
print('******************predict*********************')

# xx在-3到3之间以步长为0.1，yy在-3到3之间以步长为0.1，生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
print('xx.shape:', xx.shape)
# 将xx, yy拉直，并合并配对为二维张量，生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)

# 将网格坐标点喂入神经网络，进行预测，probs为输出
probs = []
for x_test in grid:
    # 使用训练好的参数进行预测
    h1 = tf.matmul([x_test], w1) + b1
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2
    probs.append(y)

# 取第0列给x1，取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
# squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour函数，给probs值为0.5的所有点上色  plt.show()后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

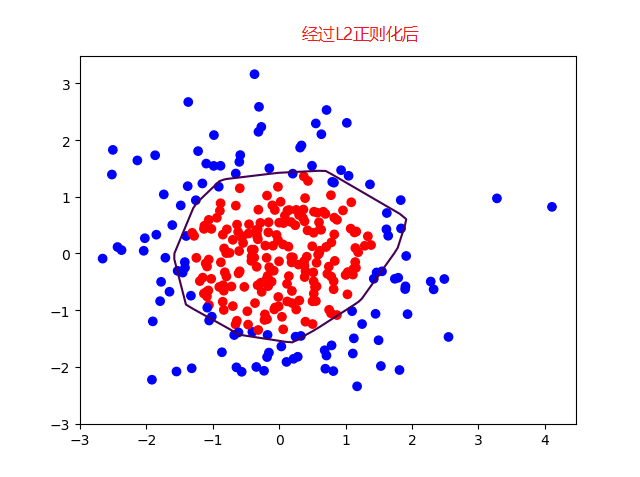
　　（2）加入L2正则化

#! /usr/bin/env python
# -*- coding:utf-8 -*-

import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

# 读入数据/标签，生成x_train, y_train
df = pd.read_csv('./datasets/dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])

x_train = np.vstack(x_data).reshape([-1, 2])
y_train = np.vstack(y_data).reshape([-1, 1])

Y_c = [['red' if y else 'blue'] for y in y_train]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)

# from_tensor_slices函数切分传入的张量的第一个维度，生成相应的数据集，使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
print(train_db)

# 生成神经网络的参数，输入层为2个神经元，隐藏层为11个神经元，1层隐藏层，输出层为1个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11], dtype=tf.float32))
b1 = tf.Variable(tf.constant(0.01, shape=[11]))

w2 = tf.Variable(tf.random.normal([11, 1], dtype=tf.float32))
b2 = tf.Variable(tf.constant(0.01, shape=[1]))

# 设置学习率
lr = 0.005
# 设置循环轮数
epochs = 800

# 训练部分
for epoch in range(epochs):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:  # 记录梯度信息
            # 记录神经网络乘加运算
            h1 = tf.matmul(x_train, w1) + b1
            # 经过激活函数reLu
            h1 = tf.nn.relu(h1)
            # 计算输出y
            y = tf.matmul(h1, w2) + b2

            # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_mse = tf.reduce_mean(tf.square(y_train - y))
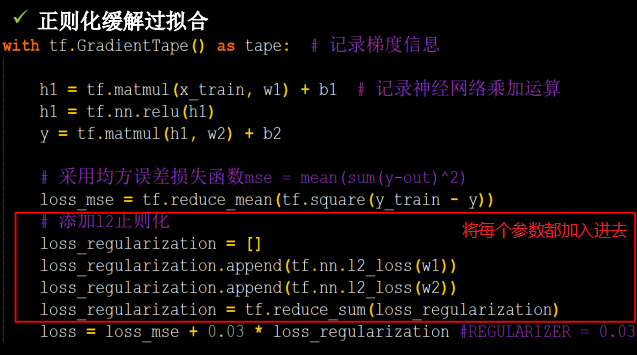
            # 添加l2正则化
            loss_regularization = []
            # tf.nn.l2_loss(w)=sum(w ** 2) / 2
            loss_regularization.append(tf.nn.l2_loss(w1))
            loss_regularization.append(tf.nn.l2_loss(w2))
            loss_regularization = tf.reduce_sum(loss_regularization)
            # REGULARIZER = 0.03
            loss = loss_mse + 0.03 * loss_regularization

        # 计算loss 对各个参数的梯度
        variables = [w1, b1, w2, b2]
        grads = tape.gradient(loss, variables)

        # 实现梯度更新
        # w1 = w1 - lr * w1_grad tape.gradient是自动求导结果与[w1, b1, w2, b2] 索引为0，1，2，3
        w1.assign_sub(lr*grads[0])
        b1.assign_sub(lr*grads[1])
        w2.assign_sub(lr*grads[2])
        b2.assign_sub(lr*grads[3])

    # 每20个epoch，打印loss
    if epoch % 20 == 0:
        print('epoch:', epoch, 'loss:', float(loss))

##################### 预测 ##############################
print('******************predict*********************')

# xx在-3到3之间以步长为0.1，yy在-3到3之间以步长为0.1，生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
print('xx.shape:', xx.shape)
# 将xx, yy拉直，并合并配对为二维张量，生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)

# 将网格坐标点喂入神经网络，进行预测，probs为输出
probs = []
for x_test in grid:
    # 使用训练好的参数进行预测
    h1 = tf.matmul([x_test], w1) + b1
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2
    probs.append(y)

# 取第0列给x1，取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
# squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour函数，给probs值为0.5的所有点上色  plt.show()后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()