1.什么是感受野?
卷积神经网络各输出层每个像素点在原始图像上的映射区域大小
下图是感受野示意图
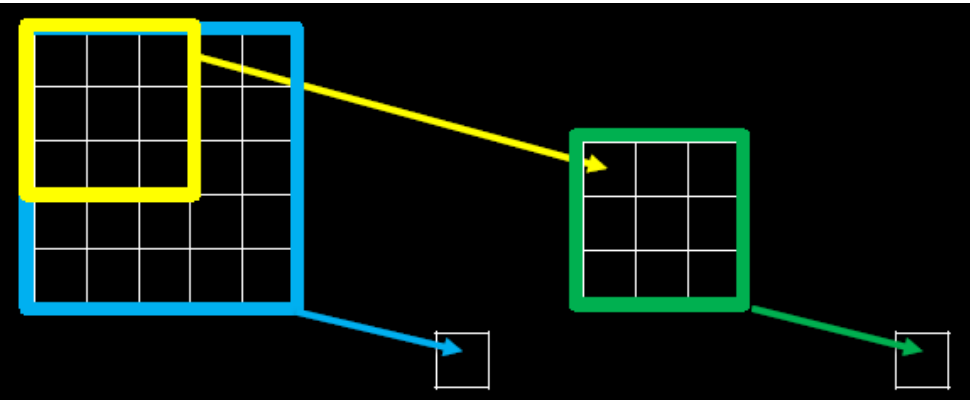
- 如果对这个5x5的原始输入图片,用黄色的3x3卷积核作用,会输出一个3x3的输出特征图,这个输出特征图上的每个像素点映射到原始的图片是3x3的区域,所以它(输出特征图)的感受野是3,如果再对这个3x3的特征图,用这个绿色的3x3卷积核作用,会输出一个1x1的输出特征图,这个输出特征图上的像素点映射到原始的图片是5*5的区域,所以这个输出特征图的感受野是5
- 如果对这个5x5的原始输入图片,用蓝色的5x5卷积核作用,会输出一个1x1的输出特征图,这个输出特征图上的像素点映射到原始的图片是5*5的区域,所以这个输出特征图的感受野也是5
同样一个5x5的原始输入图片,经过两层3x3的卷积核作用和经过一层5x5的卷积核作用都得到一个感受野是5的输出特征图,所以这两种方法的特征提取能力是一样的,那么是选择两层3x3的卷积核还是选择一层5x5的卷积核呢?
当我们采用尺寸不同的卷积核时,最大的区别就是感受野的大小不同,所以经常会采用多层小卷积核来替换一层大卷积核,在保持感受野相同的情况下减少参数量和计算量,例如十分常见的用 2 层 3 * 3 卷积核来替换 1 层 5 * 5 卷积核的方法
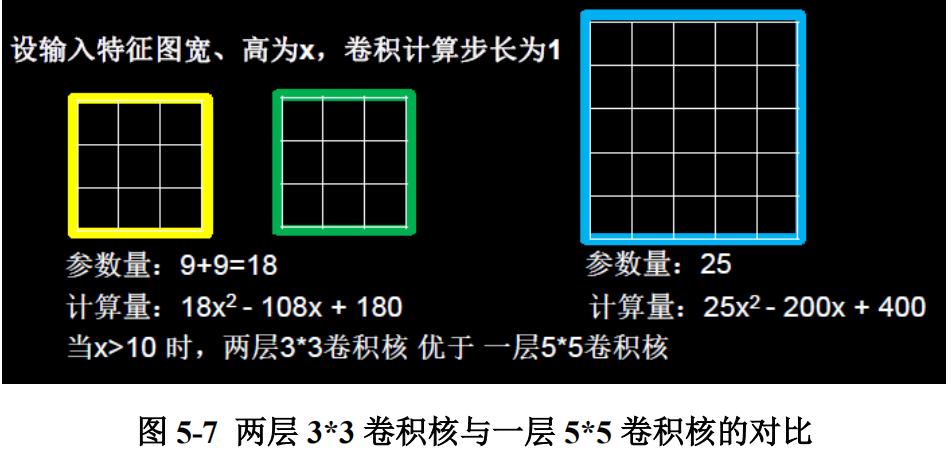
这里给出详细推导:
不妨设输入特征图的宽、高均为 x,卷积计算的步长为 1,显然,两个 3 * 3 卷积核的参数量为 9 + 9 = 18,小于 5 * 5 卷积核的 25,前者的参数量更少。
在计算量上,根据图 5-8 所示的输出特征尺寸计算公式,对于 5 * 5 卷积核来说,输出特征图共有(x – 5 + 1)^2 个像素点,每个像素点需要进行 5 * 5 = 25 次乘加运算,则总计算量为 25 * (x – 5 + 1)^2 = 25x^2 – 200x + 400;
对于两个 3 * 3 卷积核来说,第一个 3 * 3 卷积核输出特征图共有(x – 3 + 1)^2 个像素点,每个像素点需要进行 3 * 3 = 9 次乘加运算,第二个 3 * 3 卷积核输出特征图共有(x – 3 + 1 – 3+ 1)^2 个像素点,每个像素点同样需要进行 9 次乘加运算,则总计算量为 9 * (x – 3 + 1)^2 +9 * (x – 3 + 1 – 3 + 1)^2 = 18 x^2 – 108x + 180;
对二者的总计算量(乘加运算的次数)进行对比,18 x^2 – 200x + 400 < 25x^2 – 200x +400,经过简单数学运算可得 x < 22/7 or x > 10,x 作为特征图的边长,在大多数情况下显然会是一个大于 10 的值(非常简单的 MNIST 数据集的尺寸也达到了 28 * 28),所以两层 3 *3 卷积核的参数量和计算量,在通常情况下都优于一层 5 * 5 卷积核,尤其是当特征图尺寸比较大的情况下,两层 3 * 3 卷积核在计算量上的优势会更加明显。