最小顶点覆盖
定义:能覆盖所有的边的最少顶点数(或是最小点权和)
计算方法:最小顶点覆盖 = 最大匹配数
证明:
不妨把这个问题抽象为这个:
平面内有G个点((x,y)),每次可以选择一个x或y,然后删除该直线上的所有点,问最少几次可以删去所有点?
显然是以点的x坐标为集合{X},点的y坐标为集合{Y}。那么如下连边:
[1> 从S向{X}连一条流量为1的边。
[2> 从{Y}向T连一条流量为1的边。
[3> 若有点(x,y),则由 x 向 y 连接一条流量为INF的边。
显然我们要选择一些点使得[3>中连边都被控制,最少点数显然是最小割,即二分图的最大匹配。
即证毕。
最大独立集
定义:两两互不相邻的点组成的集合的最大点数(或是最大点权和)
计算方法:最大独立集 = 点总数 - 最小顶点覆盖
例题:方格取数问题(https://daniu.luogu.org/problemnew/show/2774)
我们以最大点权和(最大独立集就是点权全为1)为例证明:
一个二分图集合{X}、{Y},
[1> 从S向{X}连一条流量为点权的边。
[2> 从{Y}向T连一条流量为点权的边。
[3> 把 不能相邻或同时选的两点 之间连接一条流量为INF的边。
那么答案 = 所有点点权和 - 此二分图的最小割。
显然当S与T联通时,说明有不合法的选点。
那么对于任意一个不合法选点,要么断掉(S - {X})这条边,要么断掉({Y} - T)这条边。
这不就是最小割吗,最小割=最大流=最小顶点覆盖,即得证。
最小路径覆盖
定义:能覆盖所有点的最少路径数 [不要求为二分图]
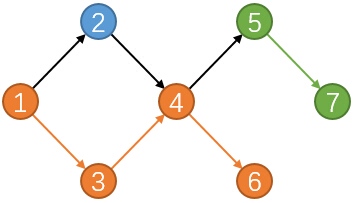
如此图的最小路径覆盖为3。
为1->3->4->6与2与5->7。(注:每个点只能到一次)。
计算方法1:最小路径覆盖 = 最大流的最小费用(特殊建图)
例题:[SDOI2010]星际竞速( https://www.luogu.org/problemnew/show/P2469)
证明1:用最小费用流证明:
把每一个点拆成 i 与 i' ,形成一个二分图,如下连边:
[1> 从S向{i}连接一条 (cap=1,cost=0) 的边。
[2> 从{i'}向T连接一条 (cap=1,cost=0) 的边。
[3> 如果a-->b在原图上有边,那么a 到 b' 连一条 (cap=1,cost=0) 的边。
[4> 从S向{i'}连一条 (cap=1,cost=1) 的边。
那么此时,每条S-->i'的边就对应选择了一条路径,费用为1,等于选择了一个起点。
最终的最少路径数为:此图的最小费用最大流的费用值。
当所求为路径权值最小时,做法一样,只需把
[4> 中连边的边的cost设为对应的从某点出发代价。
[3> 中连边的代价设为对应的路径长度。
然后一样的跑最小费用最大流,答案为最终跑出来的费用。(这个变式详见例题)
计算方法2:最小路径覆盖 = 原图上的点数 - 最大匹配数(特殊建图)
证明2:用最大流证明:
把每一个点拆成i 与 i' ,形成一个二分图,只连接法一中的[1>、[2>、[3>的边。
[1> 从S向{i}连接一条 (cap=1,cost=0) 的边。
[2> 从{i'}向T连接一条 (cap=1,cost=0) 的边。
[3> 如果a-->b在原图上有边,那么a 到 b' 连一条 (cap=1,cost=0) 的边。
然后显然每一个点会优先尝试由S流通到T,但由于[3>中cap=1的限制,有些点流通不了。
那么剩下的这些点只能作为起点 。
所以求最大匹配即求最多可流通点数,剩下的点只能作为路径起点,即为选择了一条路径。
即证毕。
最大权闭合子图
定义:给定一个有向图,从中选择一些点组成一个点集V。对于V中任意一个点,其后续节点都仍然在V中。
计算方法:最大权=所有正点和-最小割
例题:太空飞行计划问题(https://www.luogu.org/problemnew/show/2762)
证明:
一般来说,这类问题都与最佳收益有关。
这里就以这个为例,假设实验集合{X}的点选择会有收益,器材集合{Y}的点选择会有损失。
但是要选择Xi则必须选择{Ya , Yb , ....}一个{Y}的集合。问最大收益? (同例题)
我们假设{X}中的所有收益都获取到了。
那么最终答案为 总收益 - 总损失,现在我们只需要最小化总损失。
我们如下连边:
[1> 从S向{X}连一条 流量限制 为收益的边。
[2> 从{Y}向T连一条 流量限制 为损失的边。
[3> 若选Xi必须要选Yj,那么由Xi向Yj连一条 流量限制 为INF的边。
那么最小损失就是最小割。
我们可以这么理解:S表示选择,T表示不选择。
一个东西不能既选又不选,所以S->X 与 Y->T的其中一条边是一定要断掉的。
[A> 如果割掉S->X的边,则实验Xi被划分到了 不选(T) 中去,损失为实验收益(没有进行此实验,无收益)
[B> 如果割掉Y->T的边,则器材Yi被划分到了 选择(S) 中,损失为器材费用(购买了此器材)
所以当割掉最小割时,达到最优的平衡状态,为最大权闭合子图的补集。
即证毕。
最大团
定义:最大团即一个点集,点集中的点两两之间有边。
计算方法:最大团 = 补图最大独立集
补图:若原图中存在(x->y),则补图中没有 ;若原图中不存在(x->y),则补图中存在。
证明:显然若原图中,点与点之间两两有边,那么在补图中点两两之间不相邻,证完了。
最长反链 && 最小链覆盖
先明确一下关于 (DAG) 的相关概念:
(1)链:
链是一个点集,其中任意两点u,v ,
都满足 [u能到达v]+[v能到达u]=1 (就是说两个只满足其一)
(2)反链:
与链的定义类似,就是一个点集,其中的任意两个点都无法到达。
(3)最小链覆盖:
选出最少的链,使得其覆盖整个图(每条边都被覆盖至少一次)。
这里特别区分一下最小路径覆盖,最小链覆盖中,每个点是可以覆盖多次的!
(4)最长反链
即选出一个容量最大的点集,满足其中任意两点都无法到达。
.
然后一个重要的结论:
最长反链 == 最小链覆盖 ..... (非常滑稽的是我并不会证)。
然后我们如何求最小链覆盖呢?
具体做法如下:
(1)我们先跑一次传递闭包 , 把其转化为最小路径覆盖:
注释:
//cot means connect!
//Before This Step , if(u->v exist)cot[u][v]=1 ; else cot[u][v] = 0;
for(RG int k = 1; k <= n; k ++)
for(RG int i = 1; i <= n; i ++)
for(RG int j = 1; j <= n; j ++)
cot[i][j] |= (cot[i][k] & cot[k][j]);
仔细看看其实就是 (Floyed) 啦,此时我们按照最小路径覆盖的方式连边即可。
S = 0; T = 2*n+1;
for(RG int i = 1; i <= n; i ++) Add(S,i) , Add(i+n,T);
for(RG int i = 1; i <= n; i ++)
for(RG int j = 1; j <= n; j ++)
if(cot[i][j])Add(i,j+n);
Ans = n - Dinic(); //最小路径覆盖的求法
为啥子这样做是对的呢?其实也不是很难。
想想看我们现在选择的两个端点是什么?其实就是图上一条路径是吧。
你可能会问:这样做的话每个点不是只能当做一条路径的起点了吗?
其实仔细想一想,
如果一个点被多条路径经过,那么肯定可以选择一个其它的路径上的点作为起点。
所以这样子做是没有问题的。
这个玩意最经典的一道题就是: [CTSC2008]祭祀river , 把这题做一下基本上就差不多了。