0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结图内容
图存储结构
1.邻接矩阵
什么是邻接矩阵:邻接矩阵,顾名思义,就是用矩阵来存储图结构,需要我们在结构体里定义一个二维数组,利用行数与列数来表示某个点到某个点的关系

结构体定义:
typedef struct
{
int vexs[MaxV];/* 顶点表 */
int arc[MaxV][MaxV];/* 邻接矩阵,可看作边表 */
int numNodes, numEdges;/* 图中当前的顶点数和边数 */
} MGraph;
邻接矩阵的优缺点:
优点:1.能够很方便的遍历图的各个边
缺点:1.矩阵能够存储的信息有限 2.浪费空间较多,无论有没有边都需要给予内存
2.邻接表
什么是邻接表:邻接表,就是利用类似链表的结构来存储图,与普通链表不同的是,邻接表有一个头结点数组来做一条条链表的的头结点,数组里的每一个结点代表图里对应的某一个结点
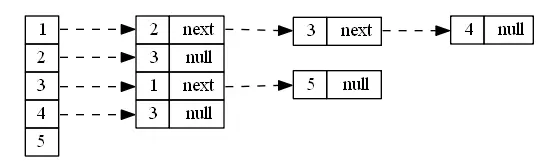
结构体定义:
typedef struct ANode //链表结点
{
int adjvex; //边所指的结点在头结点数组里对应的下标
struct ANode* nexttarc; //指向下一个结点
int info; //可存储边的信息
}ArcNode;
typedef struct Vnode //头结点
{
Vertex data; //结点数据
ArcNode * firstarc; //指向链的第一个结点
}VNode;
typedef struct //邻接表
{
VNode adjlist[MaxV]; //头结点数组
int n, e; //n为图的节点数,e为图的边数
}AdjGraph;
邻接表的优缺点:
优点:1.可以将点与边的信息都存储在邻接表里 2.有多少结点与多少边就申请多少空间,不会造成内存浪费
缺点:1.在查找边与对边的修改上较邻接矩阵麻烦,需要利用指针遍
图遍历及应用
图遍历:
1.深度优先遍历(DFS)
什么是深度优先遍历:深度优先遍历,就是在访问完一个结点后,若该结点仍有未访问过的邻接点,则往下访问该邻接点,若没有则回溯到上一个结点看有没有未访问的邻接点,重复此过程直到结束。

代码实现
邻接矩阵实现DFS:
void DFS(MGraph G, int v)
{
int i, j;
visit[v] = 1;
if (flag == 0)
{
flag = 1;
cout << v;
}
else
{
cout <<" "<< v;
}
for (j = 1; j <= G.n; j++)
{
if (G.edges[v][j] ==1 && visit[j] == 0)
{
DFS(G, j);
}
}
}
邻接表实现DFS:
void DFS(AdjGraph* G, int v)
{
ArcNode* p;
int i;
p = G->adjlist[v].firstarc;
visit[v] = 1;
if (flag == 0)
{
flag = 1;
cout << v;
}
else
{
cout << " " << v;
}
while(p!=NULL)
{
i = p->adjvex;
if (visit[i] != 1)
{
DFS(G, i);
}
p = p->nextarc;
}
}
2.广度优先遍历BFS
什么是广度优先遍历:就是在访问完第一个结点后,依次访问该结点所有未访问过的结点,再依次进入上次访问过的结点重复上述过程,直到结束。
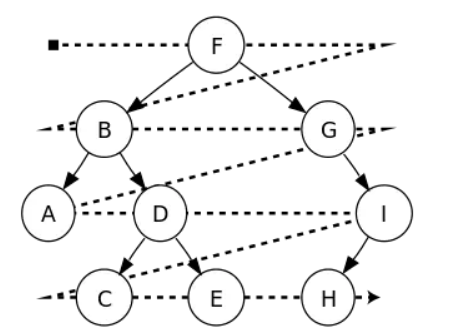
代码实现:
邻接矩阵实现BFS:
void BFS(MGraph G, int v)//广度遍历
{
int i;
queue<int> Q;
if (visit[v] == 0)
{
visit[v] = 1;
cout << v;
Q.push(v);
}
while (!Q.empty())
{
v = Q.front();
Q.pop();
for (i = 1; i <= G.n; i++)
{
if (G.edges[v][i] && visit[i] == 0)
{
visit[i] = 1;
cout << " " << i;
Q.push(i);
}
}
}
}
邻接表实现BFS:
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
queue<VNode> Q;
ArcNode* p;
visit[v]=1;
Q.push(G->adjlist[v]);
while (!Q.empty())
{
cout << Q.front.data ;
p = Q.front.firstarc;
Q.pop();
while (p!=NULL)
{
if (visit[p->adjvex] == 0)
{
Q.push(G->adjlist[p->adjvex]);
visited[p->adjvex] = 1;
}
p = p->nextarc;
}
}
}
判断图是否连通:
可以利用上述的两个遍历方法对图进行遍历,再检查visit数组是否全置为1,如果全置为1,说明全图都被遍历到了,即图为连通,否则为不连通。
查找图路径:
可以利用上述的两个遍历方法对图进行遍历,并利用一个数组path来存储结点的前驱,直到访问到目标结点停止。
找最短路径:
1.Dijkstra算法求最短路径:
定义两个数组,Dist数组为起始点到其他结点的距离,初始化时如果与起始点有边的话就修改为其边的值,如果没边置为无穷,初始化path数组除起始点的path值为自身外,其他的值都为1;从未访问的结点中选取一个对应的dist数组里值为最小的顶点,先修改其path数组里对应的值为上一个结点,然后对该结点对应的dist的距离值进行修改,如果加入该结点做中间结点后,起始点到其他顶点的距离值比原来路径要短,则修改此距离值;重复以上步骤,直到所有结点都被访问为止。
void Dijkstra(MGraph g, int v)
{
int dist[MAXV], path[MAXV];
int s[MAXV];
int mindis, i, j, u;
for (i = 0; i < g.n; i++)
{
dist[i] = g.edges[v][i];
s[i] = 0;
if (g.edges[v][i] < INF)
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
s[v] = 1;
for (i = 0; i < g.n; i++)
{
mindis = INF;
for (j = 0; j < g.n; j++)
{
if (s[j] == 0 && dist[j] < mindis)
{
u = j;
mindis = dist[j];
}
}
s[u] = 1;
for (j = 0; j < g.n; j++)
{
if (s[j] == 0)
{
if (g.edges[u][j] < INF && dist[u] + g.edges[u][j] < dist[j])
{
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
}
}
}
2.Floyd算法求最短路径:
采用矩阵来进行操作,A[],path[][],每次取一个顶点 k 为中间点,若 i 到 j 的距离大于 i 到 k 的距离加上 k 到 j 的距离,则修正A[i][j]=A[i][k]+A[k][j],path[i][j]=k。直到顶点遍历完成
for (k=0;k<g.n;k++)
{
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j])
{
A[i][j]=A[i][k]+A[k][j];
path[i][j]=k;
}
}
最小生成树相关算法及应用
1.prim算法
采用两个数组closest[]存未入选顶点距离最近的已选顶点,lowcost[]存closest[k]到k之间的距离。每次从lowcost数组中挑选最短边节点k输出(将lowcost[k]=0,表示已选),若新加入的顶点使得未加入顶点最短边有变化则修正closest跟lowcost数组。循环直到所有节点入选。
void Prim(MGraph G, int v)
{
int lowcost[MAXV], min, closest[MAXV], i, j, k;
for (i = 0; i < G.n; i++)
{
lowcost[i] = G.edges[v][i];
closest[i] = v;
}
for (i=1;i<G.n;i++)
{
min=INF;
for (j=0;j<G.n;j++)
if (lowcost[j]!=0 && lowcost[j]<min)
{
min=lowcost[j];
k=j;
}
cout>>k;
lowcost[k]=0;
for (j=0;j<G.n;j++)
if (lowcost[j]!=0 && G.edges[k][j]<lowcost[j])
{
lowcost[j]=G.edges[k][j];
closest[j]=k;
}
}
}
2.Kruskal算法:
算法将所有边权值进行排序。依次从小选取边,若选取的边没有使图形成环路,则入选该边,直到选满n-1一条边为止。
void Kruskal(AdjGraph* G, Edge E[])
{
int e=1,j=1;
int totalCost = 0;
int u1, v1,root1,root2;
while (e < G->n)
{
u1 = E[j].u;
v1 = E[j].v;
root1 = FindRoot(u1);
root2 = FindRoot(v1);
if (root1 != root2)
{
Union(E[j].u, E[j].v);
e++;
totalCost += E[j].w;
visited[E[j].u] = visited[E[j].v] = 1;
}
j++;
}
for (int i = 1; i <= G->n; i++)
{
if (!visited[i])
{
cout << "-1";
return;
}
}
cout << totalCost;
}
拓扑排序、关键路径
1.拓扑排序:
拓扑序列是指,每个顶点出现且只出现一次,且严格按照边的先后顺序来排,假如1结点指向2结点,则在序列里1必须在2之前。所以能够进行拓扑排序的图必须是有向无环图。
伪代码:
遍历图,将所以顶点的入度存入count[]数组;
遍历顶点
将入度为0的顶点入栈
while (栈不空)
{
出栈节点a;
遍历a的所有邻接点
{
入度--;
若入度为0,入栈
}
}
2.关键路径
在AOE网中,从起始点到目标点所有路径中最长路径长度的路径称为关键路径。
1.2.谈谈你对图的认识及学习体会。
图结构能将一些几何结构或者平面结构的图形数据化存储,从而解决许多诸如路径问题、图着色问题的平面图形问题,我也相信在以后通过与其他新学习的数据结构结合,能够解决更多复杂的问题。
对于图的学习,主要是通过对各个算法的掌握,如prim算法、Kruskal算法等等,本章学习内容比较紧凑,可能自己掌握地不是非常熟练,希望自己通过更多的练习来提高自己。
2.阅读代码(0--5分)
2.1 题目及解题代码
题目:
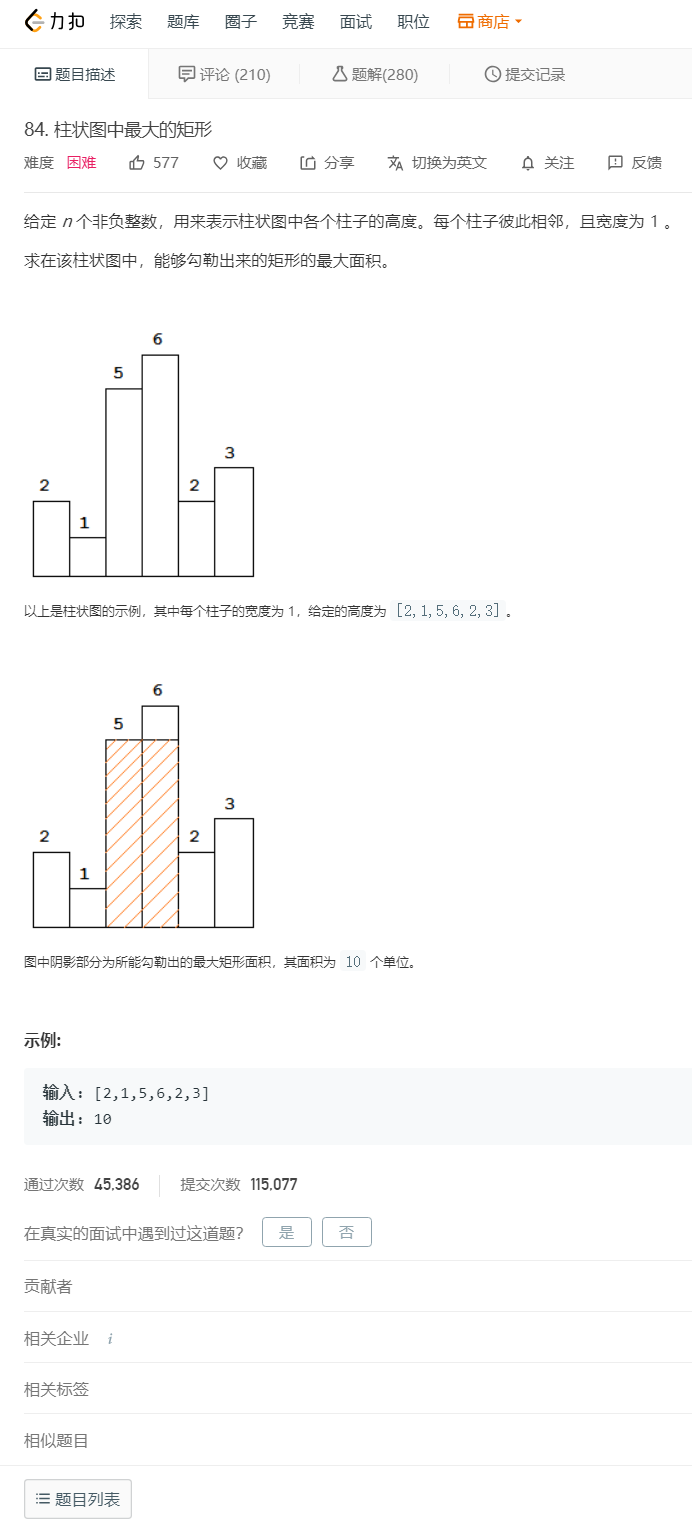
解题代码:
int largestRectangleArea(vector<int>& heights)
{
int ans = 0;
vector<int> st;
heights.insert(heights.begin(), 0);
heights.push_back(0);
for (int i = 0; i < heights.size(); i++)
{
while (!st.empty() && heights[st.back()] > heights[i])
{
int cur = st.back();
st.pop_back();
int left = st.back() + 1;
int right = i - 1;
ans = max(ans, (right - left + 1) * heights[cur]);
}
st.push_back(i);
}
return ans;
}
2.1.1 该题的设计思路
该题利用单调栈(单调栈分为单调递增栈和单调递减栈,单调递增栈即栈内元素保持单调递增的栈,同理单调递减栈即栈内元素保持单调递减的栈)里的单调递增栈来解决,在新元素小于栈顶元素时,出栈顶元素,计算新栈顶元素与新元素的距离乘以旧栈顶元素的高,即为以旧栈顶元素为高并包含栈顶元素的最大矩阵。
时间复杂度:O(n)
空间复杂度:O(n)
2.1.2 该题的伪代码
int largestRectangleArea(vector<int>& heights)
{
将0进栈
while (遍历所有高度)
{
while (栈不空 && 栈顶元素大于新元素)
{
cur = 栈顶
left = 新栈顶下标 + 1;
right = 新元素下标 - 1;
最大矩阵 = max(最大矩阵, (right - left + 1) * cur高度);
}
入栈新元素
}
}
2.1.3 运行结果
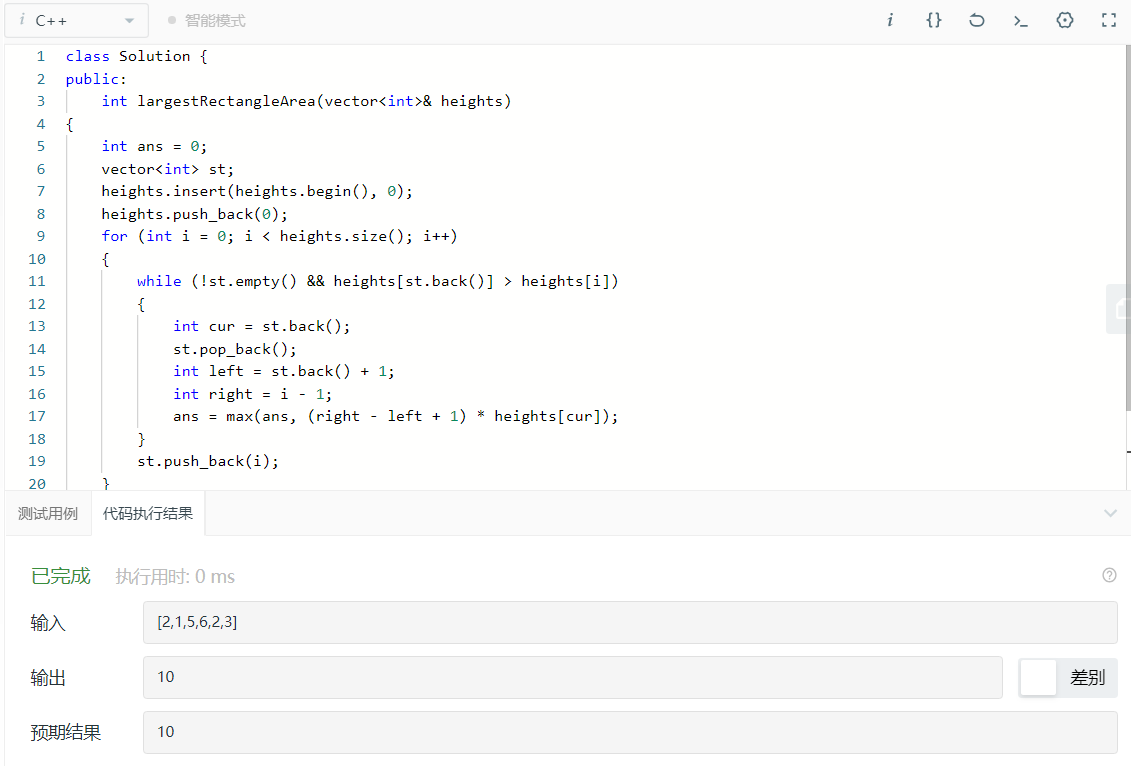
2.1.4分析该题目解题优势及难点。
解题优势:运用单调栈的特性解题,快速找到每个高度对应的宽度。
难点:每个高度对应的宽度需要找到左右界限求得宽,而高度是不确定的,所以不好寻找。
2.2 题目及解题代码
题目:
解题代码:
class Solution {
vector<bool> viewed;
vector<vector<int>> adList;
public:
bool findWhetherExistsPath(int n, vector<vector<int>>& graph, int start, int target) {
viewed = vector<bool>(n,0);
adList = vector(n,vector<int>(1,-1));
for (int i=0;i<graph.size();i++){
adList[graph[i][0]].push_back(graph[i][1]);
}
return search(start,target);
}
bool search(int start,int target){
viewed[start] = 1;
bool result = 0;
for(int i=1;i<adList[start].size();i++){
if (viewed[adList[start][i]]==0){
if(adList[start][i]==target){
viewed[adList[start][i]] =1 ;
return 1;
}
result = search(adList[start][i],target);
if(result==1)
break;
}
}
return result;
}
};
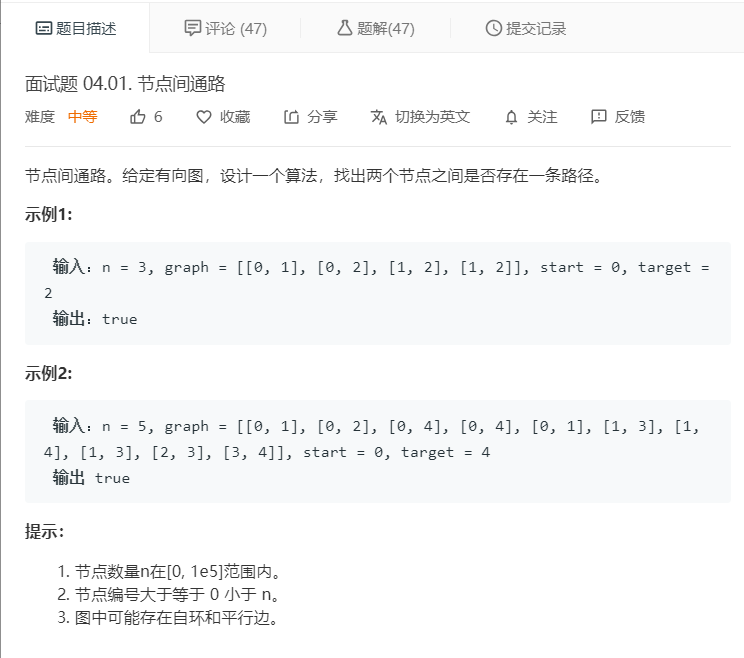
2.2.1 该题的设计思路
从start开始深度优先或广度优先搜索,如果使用邻接矩阵存储图的话,有些用例会超出内存限制,所以使用邻接表存储图。
利用DFS,从出发点开始遍历,如果遍历到目标点返回true,若访问完所有结点仍未找到目标点,则说明无路径,返回false。
时间复杂度O(n+e)
空间复杂度O(n+e)
2.2.2 该题的伪代码
search(当前结点,目标结点)
{
输入顶点数和边数
创建邻接表
输入出发点和目标点
bool result=0//用于记录结果有无路径
for(遍历邻接表的头结点)
{
for(遍历头结点的所有邻接点)
if(第一个邻接点==目标结点)
{
result=1;
return true;
}
result = search(当前结点,目标结点)//递归
}
根据result的值输出结果;
}
2.2.3 运行结果

2.2.4分析该题目解题优势及难点。
解题优势:运用递归,使算法更加简短清晰。使用邻接表来存储数据,不会浪费空间
难点:在使用递归的方法时,如果没有很好的设置递归口,很容易进入死循环。
2.3 题目及解题代码
题目:
解题代码:
class Solution {
public:
bool dfs(const vector<vector<int>>& graph, vector<int>& cols, int i, int col) {
cols[i] = col;
for (auto j : graph[i]) {
if (cols[j] == cols[i]) return false;
if (cols[j] == 0 && !dfs(graph, cols, j, -col)) return false;
}
return true;
}
bool isBipartite(vector<vector<int>>& graph) {
int N = graph.size();
vector<int> cols(N, 0);
for (int i = 0; i < N; ++i) {
if (cols[i] == 0 && !dfs(graph, cols, i, 1)) {
return false;
}
}
return true;
}
};
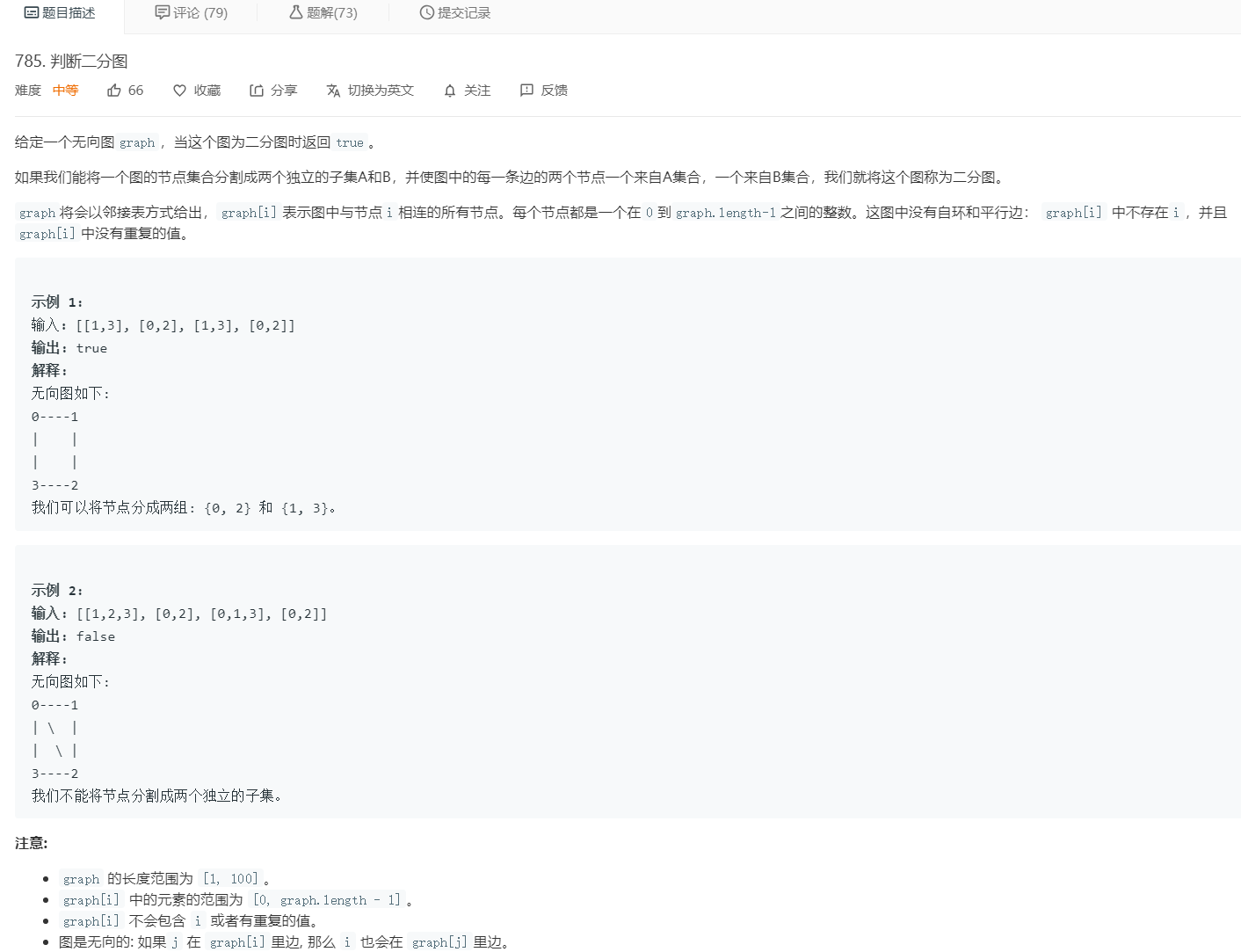
2.3.1 该题的设计思路
利用DFS染色法解决问题,在进行DFS遍历时,先将图所有结点的颜色初始化为0,然后在遍历时对颜色为0的结点以1与-1交替赋值,对已赋值的点判断两邻接点的颜色是否相同,若相同,说明图无法二分。
时间复杂度:O(n+e)
空间复杂度:O(n+e)
2.3.2 该题的伪代码
bool dfs(const vector<vector<int>>& graph, vector<int>& cols, int i, int col)
{
将起始点染色成col;
for(遍历i的邻接点)
if(邻接点颜色与i 相同) return false;
if(邻接点未被染色) 调用dfs(graph, cols, i, -col);
end for
return true;
}
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
解题优势:运用DFS染色来将结点分为两类,从而判断是否是二分图
难点:难点在于如何在递归时对下一节点的染色,判断染何色,并需要一边染色的同时一边检查判断其邻接点是否合法