题意概述:
一张有向图,在其中设置一些关键点(即题目中的逃生出口),使得删除任意一个点之后其余点都可以到达至少一个关键点。
问至少需要设置多少中关键点,有多少种设置方法。
解析:
首先,这道题要求删掉一个点,不难想到这道题与割点有关。其次,删掉一个点其他点仍然可以到达关键点就可以想到是点双联通分量。
但是,问题关键是,真的需要在每一个点双联通分量中都设置一个关键点吗?
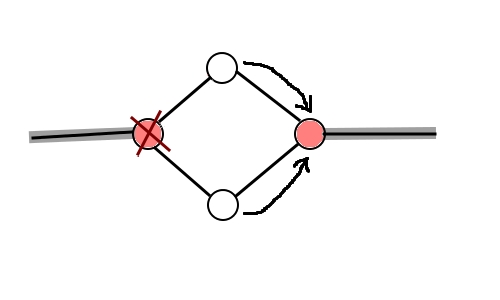
答案是否定的,因为如果一个双联通分量连接了两个或两个以上的割点,一个割点被删掉那么还可以通过另外的割点到达某个关键点,如上图,红色点为割点,灰底色的边为割边
所以只需统计含割点个数小于等于1的块数就是最少的关键点个数,如此,则放置关键点的方案数为各个被统计的块(割点数小于等于1的块)的点的个数的乘积,当然,若只找到了一个满足条件的块,那最少关键点数为2,方案数为(令n为点的个数): n*(n-1)/2.
需要注意的是这道题的数据规模:有500条边,但是并没有对点的编号的说明,所以点的标号可以是任意的,故此题建议离散化,但是我还是偷了个懒,因为数据中的点好像不超过50000
代码如下:

1 #include <iostream> 2 #include <algorithm> 3 #include <cstdio> 4 #include <cstring> 5 #include <cstdlib> 6 #include <cmath> 7 #include <ctime> 8 #include <vector> 9 10 using namespace std; 11 12 //#define File 13 //#define Debug 14 15 struct Edge 16 { 17 int to; 18 int next; 19 }e[2100]; 20 21 int n,cnt,cnt_blocks,bcc_cnt,top,Ans,kase; 22 int p[51000],dfn[51000],nbcc[51000]; 23 24 long long Sum; 25 26 pair<int,int> st[51000]; 27 vector<int> bcc[1100]; 28 29 bool cut[51000]; 30 31 inline void Add_edge(const int x,const int y) 32 { 33 e[++cnt].to=y; 34 e[cnt].next=p[x]; 35 p[x]=cnt; 36 return ; 37 } 38 39 int Tarjan(const int S,const int fa) 40 { 41 int child,lowu,lowv,v,i; 42 43 dfn[S]=lowu=++cnt_blocks; 44 child=0; 45 46 for(i=p[S];i;i=e[i].next) 47 { 48 v=e[i].to; 49 if(!dfn[v]) 50 { 51 st[++top]=make_pair(S,v); 52 child++; 53 lowv=Tarjan(v,S); 54 lowu=min(lowv,lowu); 55 if(lowv>=dfn[S]) 56 { 57 cut[S]=true; 58 bcc_cnt++; 59 bcc[bcc_cnt].clear(); 60 while(true) 61 { 62 if(nbcc[st[top].first]!=bcc_cnt) 63 { 64 bcc[bcc_cnt].push_back(st[top].first); 65 nbcc[st[top].first]=bcc_cnt; 66 } 67 if(nbcc[st[top].second]!=bcc_cnt) 68 { 69 bcc[bcc_cnt].push_back(st[top].second); 70 nbcc[st[top].second]=bcc_cnt; 71 } 72 73 if(st[top].first==S && st[top].second==v) 74 {top--;break;} 75 top--; 76 } 77 } 78 } 79 else if(dfn[v]<dfn[S] && v!=fa) 80 { 81 st[++top]=make_pair(S,e[i].to); 82 lowu=min(lowu,dfn[v]); 83 } 84 } 85 86 if(fa<0 && child==1)cut[S]=false; 87 return lowu; 88 } 89 90 inline void Init() 91 { 92 /*int n,cnt,cnt_blocks,bcc_cnt,top,Ans,kase; 93 int p[51000],dfn[51000],nbcc[51000]; 94 95 long long Sum; 96 97 pair<int,int> st[51000]; 98 vector<int> bcc[1100]; 99 100 bool visited[51000],cut[51000];*/ 101 cnt=cnt_blocks=bcc_cnt=top=Ans=0; 102 Sum=1; 103 memset(p,0,sizeof(p)); 104 memset(dfn,0,sizeof(dfn)); 105 memset(nbcc,0,sizeof(nbcc)); 106 memset(cut,0,sizeof(cut)); 107 for(int i=1;i<=1000;++i) 108 bcc[i].clear(); 109 memset(st,0,sizeof(st)); 110 return ; 111 } 112 113 114 int main() 115 { 116 #ifdef File 117 freopen("2730.in","r",stdin); 118 #ifndef Debug 119 freopen("2730.out","w",stdout); 120 #endif 121 #endif 122 123 int i,j,x,y,cut_cnt; 124 125 while(~scanf("%d",&n) && n) 126 { 127 Init(); 128 for(i=1;i<=n;++i) 129 { 130 scanf("%d%d",&x,&y); 131 Add_edge(x,y); 132 Add_edge(y,x); 133 } 134 135 for(i=1;i<=n;++i) 136 { 137 if(!dfn[i])Tarjan(i,-1); 138 } 139 140 for(i=1;i<=bcc_cnt;++i) 141 { 142 cut_cnt=0; 143 for(j=0;j<(int)bcc[i].size();++j) 144 { 145 if(cut[bcc[i][j]])cut_cnt++; 146 } 147 if(cut_cnt==1) 148 { 149 Ans++; 150 Sum*=(long long)(bcc[i].size()-cut_cnt); 151 } 152 } 153 154 if(bcc_cnt==1) 155 { 156 Ans=2; 157 Sum=bcc[1].size()*(bcc[1].size()-1)/2; 158 } 159 160 printf("Case %d: %d %lld ",++kase,Ans,Sum); 161 } 162 163 #ifdef File 164 fclose(stdin); 165 #ifndef Debug 166 fclose(stdout); 167 #endif 168 #endif 169 170 return 0; 171 }
