8.12动态规划例题：01背包之dp解法

/*
有n个重量和价值分别为wi，vi的物品，从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值。
    1≤n≤100
    1≤wi，vi≤100
    1≤W≤10000

输入：
    n=4
    (w,v)={(2,3),(1,2),(3,4),(2,2)}
    W=5

输出：
    7（选择第0，1，3号物品）

因为对每个物品只有选和不选两种情况，所以这个问题称为01背包。
 */

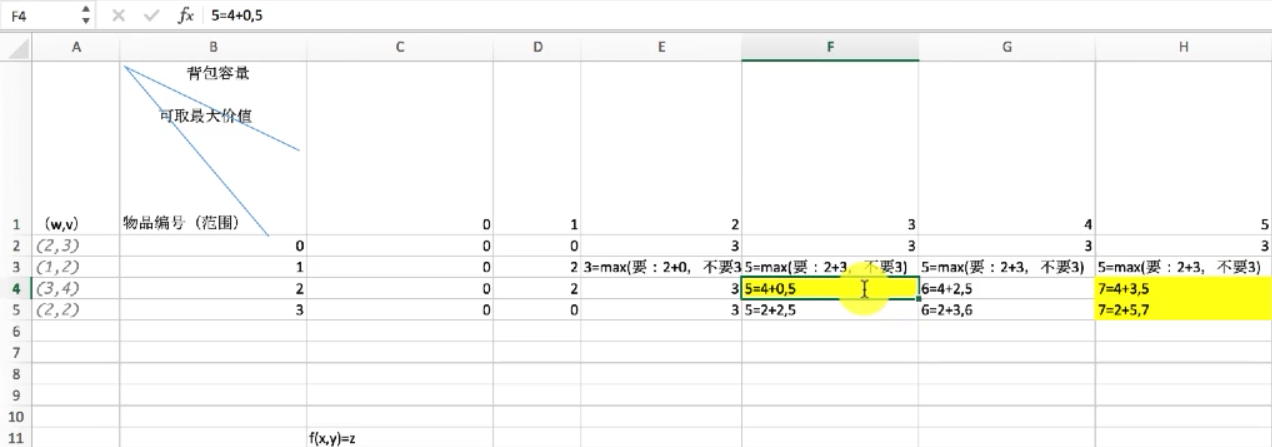
思路：
每个格子有两种选择要或者不要。第一行只有一个物品可选如果容量不够就为0，如果够当前物品就直接为当前物品的价值，其他行，要：当前列的容量必须 >= 当前可选物品的容量（当前物品的价值 + dp[上一行][当前列的容量-当前物品的容量]），如果不要当前格子直接填当前列上一行的max。

import java.util.Arrays;

public class Eight_12动态规划例题_01背包之dp解法 {
    static int n = 4;
    static int[] w = {2,1,3,2};
    static int[] v = {3,2,4,2};
    static int c = 5;
    
    private static int dp(){
        int[][] dp = new int[n][c+1];
        //初始化dp表的第一行
        for(int i = 0; i < c+1; i++){
            if(i >= w[0]) //每种容量的0号物品
                dp[0][i] = v[0];
            else
                dp[0][i] = 0;
        }
        
        //其他行
        for(int i = 1; i < n; i++){
            for(int j = 0; j < c+1; j++){
                if(j >= w[i]){    //要的起
                    int i1 = v[i] + dp[i-1][j-w[i]];    //选择当前物品即i号物品，剩余容量
                    int i2 = dp[i-1][j]; //不选择
                    dp[i][j] = Math.max(i1, i2);
                }else{
                    dp[i][j] = dp[i-1][j];
                }
                    
            }
        }
        /*for(int i = 0; i < n; i++){
            System.out.println(Arrays.toString(dp[i]));
        }*/
        return dp[n-1][c];
    }
    public static void main(String[] args) {
        System.out.println(dp());
    }
}