题意
给定一棵(n)阶树,给定一个长度为(n)的序列({a_i}),(a_i)表示点(i)的权值
(q)次询问,每次给定(l,r),求点权在([l,r])间的点集构成的斯坦纳树大小
(nle 10^5,qle 5 imes 10^5,1le a_i,l,rle 10^9)
前置
通过简单的离散化,问题可以描述成:
给定一棵(n)阶树
(q)次询问,每次给定(l,r),求集合({x|xin[l,r]}xin[l,r])的斯坦纳树大小
钦定(1)为树根
以下假定大家都会(O(nlogn))预处理,(O(1))查询({x|xin[l,r]}xin[l,r])的lca
定义:令(f(S))为集合(S)的斯坦纳树大小;令(lca(S))为集合(S)的lca;令(dep(x))为点(x)到根的路径长度
那么(f(S)=f(S+{root})-dep(lca(S)))
以下考虑如何求(f(S+{root}))
做法一
将询问离线,挂到(r)上
考虑从(1sim n)加入点,维护一个这样的东西:
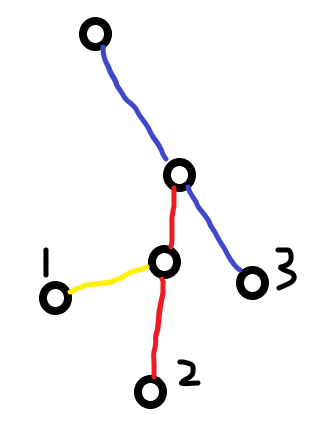
每个点会至多属于一个点(可能不属于任何点)
每个点到根有一段属于自己的路径,当加入点(i),(i)到根的路径全部属于自己
那么当加入点(i),查询([l,r](r=i)),就是查询点(j(j in[l,r]))属于(j)的点之和
这个可以用lct与树状数组来维护
做法二
考虑(f(S+{root}))中的点,一个点存在贡献当且仅当子树内有([l,r])中的点
将子树内的点排序({a_1,a_2,cdots,a_m}(a_i<a_{i+1}))
为了方便,在子树两端添加(-infty,infty):({a_0=-inf,a_1,a_3cdots,a_m,a_{m+1}=infty})
一个点没有贡献当且仅当:(exists xin[0,m]),(s.t.~a_x<l,a_{x+1}>r)
容易发现至多存在一个(x)满足此条件
我们将((a_x,a_{x+1}))看作点,求出所有子树的可重点集
那么我们将问题转化为了数点问题
但可重点集大小是(O(n^2))的,怎么解决呢?
结论:点集的大小是(O(nlogn))
利用启发式合并的过程容易证明
我们考虑用线段树合并维护点集,这里用到了一个小trick:
令([l,r])为线段树中点(nod)的区间,令({a_1,a_2,cdots,a_m})为([l,r])中的有效点集
用(tag_{nod})表示线段树中点(nod)中的有效点集中相邻点对出现了(tag_{nod})次
在下传标记的同时,将(nod)左儿子的最大值与右儿子的最小值组成的点加入可重点集,其出现的次数为(tag_{nod})
以上两种做法的时间复杂度均为(O(nlog^2n+qlogn))
加强原问题
给定一棵(n)阶树,给定一个长度为(n)的序列({a_i}),(a_i)表示点(i)的权值
给定(m),有(m)条路径,每条路径描述成((x,y)),表示(x)到(y)的最短路径
给定(q),(q)次查询,每次给定((l,r)),求([l,r])这些路径的并的点集和
这题仍然可以用做法一实现,但无法用做法二
下面介绍另一种解决的方法
考虑分治,对于([l,r]),解决(lle l'le mid<r'le r)的((l',r'))的询问:
处理出([l,r])路径有关的节点,建虚树
扫描(mid+1sim r),对虚树上路径及点记录最早被覆盖的位置,用并查集优化
将询问按(l')降序排列
扫描(i=midsim l),对于当前路径(i),若其在虚树中的路径未被(i<j(i<jle mid))覆盖,但被(j(mid+1le jle r))覆盖,则将贡献移至(i),同样用并查集优化
(O(mlog^2n+qlogn))