还是老规矩,传送门 hdu 1542
不做过多解释了,就是给出n个矩形,求出这些矩形所覆盖的面积和。由于n很小,因而这道题不是必须用线段树
先想想怎么办,先来一个例图(稍微有点复杂)
根据数学知识,我们可以像这样:
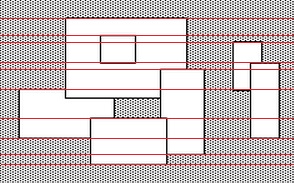
将它用红线分割,然后维护每条红线被矩形覆盖的部分的长度,然后乘以两条红线之间的距离,最后累加每一部分的面积而得到答案,没什么问题吧。
接下来,问题转化为维护线段的长度了,于是我们考虑线段树,但我们发现了一个重大问题:x坐标是实数,不能直接用线段树维护,但我们不虚,把浮点离散成整数不就好了吗。
然后,重中之重来了,线段树里存什么:
(1):存节点是否被覆盖:用脑子思考一下,就会发现这不对:例如,离散后最大坐标为6,插入一条线段[2,6],那么3,4之间的一段就消失了,必然WA,就算用强大的码力解决了这个问题,代码也必然会十分恶心,因此,我们不要这样存储
(2):存一段线是否被覆盖:这是正确的,但鉴于鄙人语文不太好,难以用语言解释,上一张图:
例如,离散后最大坐标为6,则我们要这样:
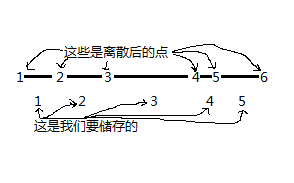
然而,我为了代码好写,传参数时传的依然是离散后的点坐标,因此,dis(L,R)=val[R+1]-val[L],
接下来,就是对线段树进行改造,使之能正确维护线段长度
我们可以这样考虑,在矩形下侧的边进入时,加一,而在上侧的边进入时,加负一,然后,对线段树进行修改,每一个节点中记录这个区间被完全覆盖的次数和被覆盖的长度,
求解前,对2n条边按高度排序,从最低的边开始,逐个枚举到最高的一条边,累加答案即可。
大体的思路有了,但我还要多说两句:
1.输出时两组之间有空行,每组的两行之间没有空行,正确的输出语句应该像下面这样
printf("Test case #%d Total explored area: %.2lf ",cas,ans);
其中:cas记录这是第几组数据,ans为这组数据的结果
2.这道题不建议大家使用万能头文件,因为y1在cmath中是一个函数,这样做会导致CE,当然,强烈不建议手欠打上
#include<cmath>
习惯不用y1的神犇们请忽略此条建议。
好了,奉上代码
1 #include<cstdio> 2 #include<map> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 map<double,int> mp; 7 double ls[5000],x1,x2,_y1,y2; 8 int n,cnt,cd; 9 struct edge 10 { 11 int l,r,val; 12 double ll,rr,h; 13 }eds[2500]; 14 struct node 15 { 16 int cov; 17 double dis; 18 }tre[2500]; 19 int cmp(edge a,edge b){return a.h<b.h;} 20 void init() 21 { 22 cnt=1; 23 cd=1; 24 mp.clear(); 25 memset(ls,0,sizeof(ls)); 26 //由于每次树都会被正好加成0,不用对树进行重置 27 } 28 int fd(double tar) 29 { 30 int l=1,r=cd; 31 while(l<r) 32 { 33 int mid=(l+r)/2; 34 if(ls[mid]<tar) 35 { 36 l=mid+1; 37 } 38 else 39 { 40 r=mid; 41 } 42 } 43 return l; 44 } 45 void pushup(int L,int R,int nc) 46 { 47 if(tre[nc].cov) 48 { 49 tre[nc].dis=ls[R+1]-ls[L]; 50 } 51 else 52 { 53 if(L==R) 54 { 55 tre[nc].dis=0; 56 } 57 else 58 { 59 tre[nc].dis=tre[2*nc].dis+tre[2*nc+1].dis; 60 } 61 } 62 } 63 void ins(int l,int r,int dt,int nc,int L,int R) 64 { 65 if(l<=L&&r>=R) 66 { 67 tre[nc].cov+=dt; 68 if(tre[nc].cov) 69 { 70 tre[nc].dis=ls[R+1]-ls[L]; 71 } 72 else 73 { 74 if(L==R) 75 { 76 tre[nc].dis=0; 77 } 78 else 79 { 80 tre[nc].dis=tre[2*nc].dis+tre[2*nc+1].dis; 81 } 82 } 83 return; 84 } 85 int mid=(L+R)/2; 86 if(l<=mid) 87 { 88 ins(l,r,dt,2*nc,L,mid); 89 } 90 if(r>mid) 91 { 92 ins(l,r,dt,2*nc+1,mid+1,R); 93 } 94 pushup(L,R,nc); 95 } 96 int main() 97 { 98 int cas=1; 99 while(1) 100 { 101 scanf("%d",&n); 102 if(n==0) 103 { 104 return 0; 105 } 106 init(); 107 for(int i=1;i<=n;i++) 108 { 109 scanf("%lf%lf%lf%lf",&x1,&_y1,&x2,&y2); 110 eds[cnt].h=_y1; 111 eds[cnt].ll=x1; 112 eds[cnt].rr=x2; 113 eds[cnt].val=1; 114 cnt++; 115 eds[cnt].h=y2; 116 eds[cnt].ll=x1; 117 eds[cnt].rr=x2; 118 eds[cnt].val=-1; 119 cnt++; 120 if(!mp[x1]) 121 { 122 mp[x1]=1; 123 ls[cd]=x1; 124 cd++; 125 } 126 if(!mp[x2]) 127 { 128 mp[x2]=1; 129 ls[cd]=x2; 130 cd++; 131 } 132 } 133 sort(ls+1,ls+cd); 134 for(int i=1;i<cnt;i++) 135 { 136 eds[i].l=fd(eds[i].ll); 137 eds[i].r=fd(eds[i].rr); 138 }//从读入到这里都是离散化 139 sort(eds+1,eds+cnt,cmp); 140 double last=eds[1].h,ans=0; 141 ins(eds[1].l,eds[1].r-1,eds[1].val,1,1,cd-1); 142 for(int i=2;i<cnt;i++) 143 { 144 ans+=(eds[i].h-last)*tre[1].dis; 145 ins(eds[i].l,eds[i].r-1,eds[i].val,1,1,cd-1); 146 last=eds[i].h; 147 } 148 printf("Test case #%d Total explored area: %.2lf ",cas,ans); 149 cas++; 150 } 151 }