2018 ACM-ICPC 中国大学生程序设计竞赛线上赛:https://www.jisuanke.com/contest/1227
题目链接:https://nanti.jisuanke.com/t/26219
Rock Paper Scissors Lizard Spock
Description:
Didi is a curious baby. One day, she finds a curious game, which named Rock Paper Scissors Lizard Spock.
The game is an upgraded version of the game named Rock, Paper, Scissors. Each player chooses an option . And then those players show their choices that was previously hidden at the same time. If the winner defeats the others, she gets a point.
The rules are as follows.
Scissors cuts Paper
Paper covers Rock
Rock crushes Lizard
Lizard poisons Spock
Spock smashes Scissors
Scissors decapitates Lizard
Lizard eats Paper
Paper disproves Spock
Spock vaporizes Rock
(and as it always has) Rock crushes Scissors.
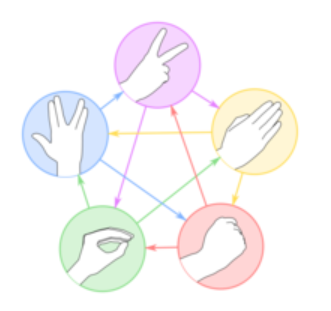
(this pic is from baike.baidu.com)
But Didi is a little silly, she always loses the game. In order to keep her calm, her friend Tangtang writes down the order on a list and show it to her. Didi also writes down her order on another list, like
.
(Rock-R Paper-P Scissors-S Lizard-L Spock-K)
However, Didi may skip some her friends' choices to find the position to get the most winning points of the game, like

Can you help Didi find the max points she can get?
Input:
The first line contains the list of choices of Didi's friend, the second line contains the list of choices of Didi.
(1<=len(s2)<=len(s1)<=1e6)
Output:
One line contains an integer indicating the maximum number of wining point.
忽略每行输出的末尾多余空格
样例输入1
RRRRRRRRRLLL
RRRS
样例输出1
3
样例输入2
RSSPKKLLRKPS
RSRS
样例输出2
2
ACM-ICPC Asia Training League 宁夏理工学院
题解:
因为之前做过codeforces 528D. Fuzzy Search ,感觉就不难了,你要是不会这题可以先去做cf528d,有个详细的题解:https://blog.csdn.net/u013368721/article/details/45565729
【FFT求字符串匹配的问题一般都是将模式串反转,然后将其与主串进行卷积运算】
枚举五种出拳方式,每种都做fft,最后扫一遍最大值即可求出最佳匹配出的赢的最大次数。(具体fft原理不懂orz,我就是套着原来板子写的...)
#include<bits/stdc++.h>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long ll;
const int N = 1<<20;
const double PI = acos(-1.0);
int n, m;
struct Complex {
double x,y;
Complex(double _x = 0.0,double _y = 0.0){
x = _x; y = _y;
}
Complex operator -(const Complex &b)const{
return Complex(x-b.x,y-b.y);
}
Complex operator +(const Complex &b)const{
return Complex(x+b.x,y+b.y);
}
Complex operator *(const Complex &b)const{
return Complex(x*b.x-y*b.y,x*b.y+y*b.x);
}
Complex operator * (const double &b)const{
return Complex(x * b,y * b);
}
Complex operator / (const double &b)const{
return Complex(x / b,y / b);
}
};
void change(Complex y[], int len) {
int i, j, k;
for(i = 1, j = len/2;i <len-1;i++) {
if(i < j)swap(y[i],y[j]);
k = len/2;
while(j >= k) {
j -= k;
k /= 2;
}
if(j < k) j += k;
}
}
void fft(Complex y[],int len,int on) {
change(y,len);
for(int h = 2; h <= len; h <<= 1) {
Complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j = 0;j < len;j+=h) {
Complex w(1,0);
for(int k = j;k < j+h/2;k++) {
Complex u = y[k];
Complex t = w*y[k+h/2];
y[k] = u+t;
y[k+h/2] = u-t;
w = w*wn;
}
}
}
if(on == -1)
for(int i = 0;i < len;i++)
y[i].x /= len;
}
Complex a[N], b[N], c[N];
char s[N], t[N];
int sum[N];
int main() {
int i, j, ans = 0, ma, nn;
scanf("%s %s", s, t);
n = strlen(s);
m = strlen(t);
reverse(t, t+m);
ma = max(n, m); nn = 1;
while(nn < 2 * ma) nn<<=1;
CLR(c, 0); CLR(sum, 0);
//R vs L S
CLR(a, 0); CLR(b, 0);
for(i = 0; i < n; ++i) a[i].x = (s[i]=='L'||s[i]=='S');
for(i = 0; i < m; ++i) b[i].x = (t[i]=='R');
fft(a, nn, 1); fft(b, nn, 1);
for(i = 0; i < nn ;++i) c[i] = a[i] * b[i];
fft(c, nn, -1);
for(i = m-1; i < n; ++i)
sum[i] += (int)(c[i].x+0.5);
//P vs R K
CLR(a, 0); CLR(b, 0);
for(i = 0; i < n; ++i) a[i].x = (s[i]=='R'||s[i]=='K');
for(i = 0; i < m; ++i) b[i].x = (t[i]=='P');
fft(a, nn, 1); fft(b, nn, 1);
for(i = 0; i < nn ;++i) c[i] = a[i] * b[i];
fft(c, nn, -1);
for(i = m-1; i < n; ++i)
sum[i] += (int)(c[i].x+0.5);
//S vs P L
CLR(a, 0); CLR(b, 0);
for(i = 0; i < n; ++i) a[i].x = (s[i]=='P'||s[i]=='L');
for(i = 0; i < m; ++i) b[i].x = (t[i]=='S');
fft(a, nn, 1); fft(b, nn, 1);
for(i = 0; i < nn ;++i) c[i] = a[i] * b[i];
fft(c, nn, -1);
for(i = m-1; i < n; ++i)
sum[i] += (int)(c[i].x+0.5);
//L vs P K
CLR(a, 0); CLR(b, 0);
for(i = 0; i < n; ++i) a[i].x = (s[i]=='P'||s[i]=='K');
for(i = 0; i < m; ++i) b[i].x = (t[i]=='L');
fft(a, nn, 1); fft(b, nn, 1);
for(i = 0; i < nn ;++i) c[i] = a[i] * b[i];
fft(c, nn, -1);
for(i = m-1; i < n; ++i)
sum[i] += (int)(c[i].x+0.5);
//K vs R S
CLR(a, 0); CLR(b, 0);
for(i = 0; i < n; ++i) a[i].x = (s[i]=='R'||s[i]=='S');
for(i = 0; i < m; ++i) b[i].x = (t[i]=='K');
fft(a, nn, 1); fft(b, nn, 1);
for(i = 0; i < nn ;++i) c[i] = a[i] * b[i];
fft(c, nn, -1);
for(i = m-1; i < n; ++i)
sum[i] += (int)(c[i].x+0.5);
for(i = m-1; i < n; ++i) ans = max(ans, sum[i]);
printf("%d
", ans);
return 0;
}