P1154 奶牛分厩

题目链接

题面:

换句话说:

　　给定n和长度为n的数组a ， 你要求出最小的k使得，没有两个a[i] 、a[j] 会满足：a[i] % k = a[j] % k

思路:

　　

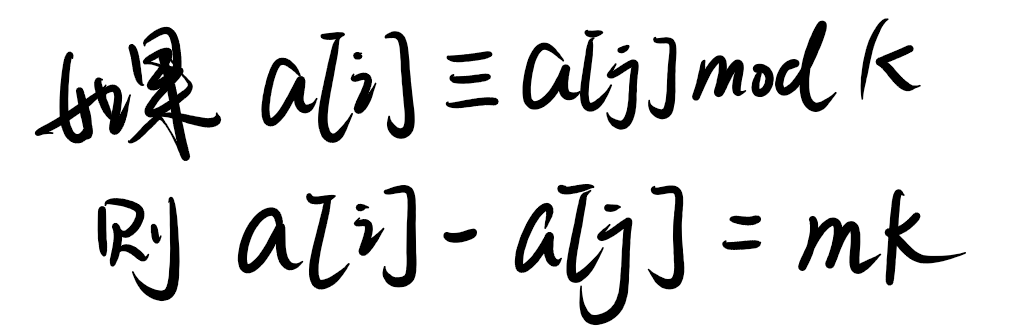
　　所以，求出数组a的两两差值x，x的所有因子都不满足条件

　　然后遍历找第一个满足条件的k

代码:

　　一开始是枚举差值，找他的所有因子进行标记，但是开了o2还是又一个点T，这是90分的代码：

　　

#include<bits/stdc++.h>
using namespace std;
const int maxn =  1e6 + 10;
#define ll long long
#define ios std::ios::sync_with_stdio(false)
const ll INF(0x3f3f3f3f3f3f3f3fll);
const int inf(0x3f3f3f3f);

int a[maxn];
int cha[maxn];
int ans[maxn];
vector<int>vec[maxn];
int vis[maxn];
signed main()
{
    ios;
    cin.tie(0);
    int n;
    cin >> n;
    for(int i = 1 ; i <= n ; i ++) cin >> a[i];
    for(int i = 1 ; i <= n ; i ++){
        for(int j = i + 1 ; j <= n ; j ++){
            int now = abs(a[j] - a[i]);
            if(vis[now])continue;
            vis[now] ++;
            ans[now] ++;
            for(int k = 2 ; k * k <= now ; k ++){
                if(now % k == 0){
                    ans[k] ++;
                    if(now / k != k) ans[now / k] ++;
                }
            }
        }
    }
    for(int i = n ; i <= 1e6 ; i ++){
        if(!ans[i]){
            cout << i <<'
';
            break;
        }
    }
    return 0;
}

　　后来看了题解别人的写法发现 , 先标记下差值，然后从n开始枚举k , 判断k的倍数是否被标记过 ， 如果没有，就是答案，这样就过了QAQ ， 这是AC的：

#include<bits/stdc++.h>
using namespace std;
const int maxn =  1e6 + 10;
#define ll long long
#define ios std::ios::sync_with_stdio(false)
const ll INF(0x3f3f3f3f3f3f3f3fll);
const int inf(0x3f3f3f3f);

int a[maxn];
int cha[maxn];
int ans[maxn];
vector<int>vec[maxn];
int vis[maxn];
signed main()
{
    ios;
    cin.tie(0);
    int n , maxx = 0;
    cin >> n;
    for(int i = 1 ; i <= n ; i ++) cin >> a[i] , maxx = max(maxx , a[i]);
    for(int i = 1 ; i <= n ; i ++){
        for(int j = i + 1 ; j <= n ; j ++){
            int now = abs(a[j] - a[i]);
            if(vis[now])continue;
            vis[now] ++;
            ans[now] ++;
        }
    }
    for(int i = n ; i <= maxx ; i ++){
        bool ok = true;
        for(int j = i ; j <= maxx ; j += i){
            if(ans[j]){
                ok = false;
                break;
            }
       }
       if(ok){
            cout << i << '
';
            break;
       }
    }
    return 0;
}