P1445 [Violet]樱花

题目链接

题意：给定n

思路：

根据唯一分解定理：

可以把C分解为：

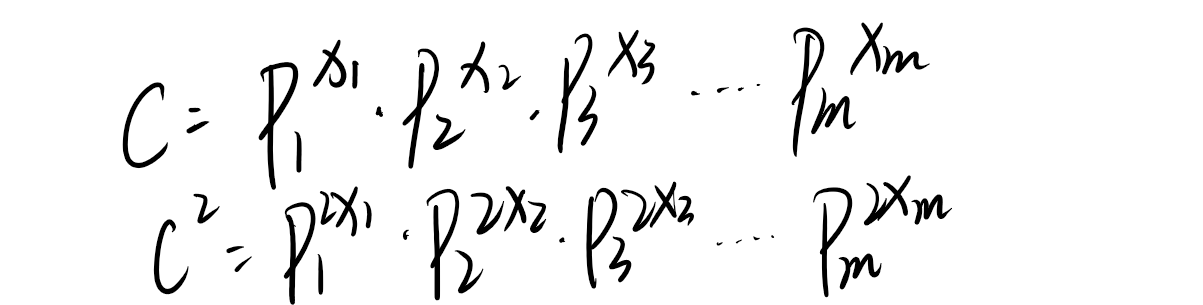
确定a之后b也可以确定下来，所以a可以怎么选：

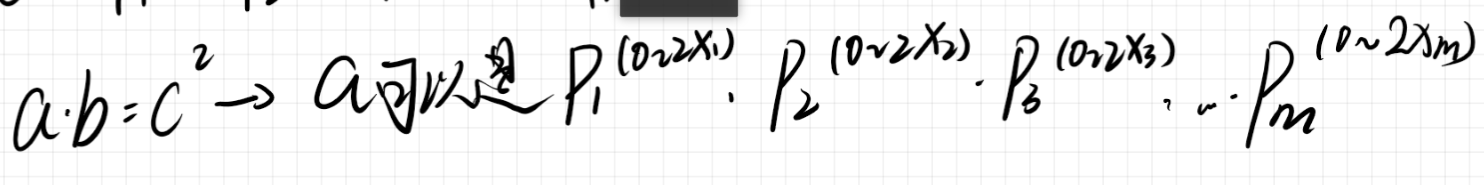
所以a的选取个数是：

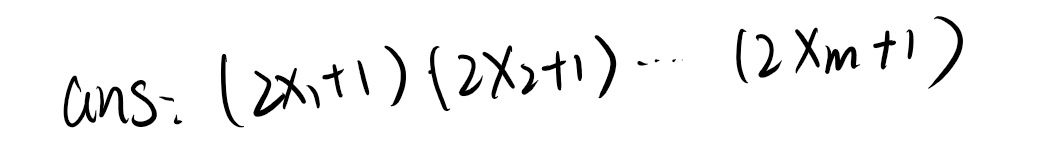
 代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn =  1e6 + 100;
#define ll long long
#define ios std::ios::sync_with_stdio(false)
const ll INF(0x3f3f3f3f3f3f3f3fll);
const int inf(0x3f3f3f3f);
#define int long long
const int mod = 1e9 + 7;
int prime[maxn],minprime[maxn];
int euler(int n)
{
    int c=0,i,j;
    for(i=2; i<=n; i++)
    {
        if(!minprime[i])prime[++c]=i,minprime[i]=i;
        for(j=1; j<=c&&i*prime[j]<=n; j++)
        {
            minprime[i*prime[j]]=prime[j];
            if(i%prime[j]==0)break;
        }
    }
    return c;
}
int cnt[maxn];
signed main()
{
    ios,cin.tie(0);
    int n;
    cin >> n;
    int nn = 1;
    int num = euler(1e6 + 10);
    for(int i = 2 ; i <= n ; i ++){
        int now = i;
        for(int j = 1 ; j <= num && prime[j] * prime[j] <= now ; j ++){
            int c = 0;
            while(now % prime[j] == 0){
                now /= prime[j] , c ++;
            }
            cnt[prime[j]] += c;
        }
        if(now > 1) cnt[now] ++;
    }
    int ans = 1;
    for(int i = 1 ; i <= 1e6 ; i ++){
        if(cnt[i]) ans *= (cnt[i] * 2 + 1) % mod;
        ans %= mod;
    }
    cout << ans % mod << '
';
    return 0;
}