Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1: Input: "babad" Output: "bab" Note: "aba" is also a valid answer.
Example 2: Input: "cbbd" Output: "bb"
思路:最简单的办法是使用暴力破解法,依此遍历每一个字符(基数情况)和相邻的两个字符(偶数情况)的情况来对比前后是最长相等的字符串,最后返回结果。但是时间复杂度太高为O(n3),如果字符串太长会直接超时。
第二种是使用动态规划,我们使用辅助数组来存储回文情况,如果在判断P(i, j)时,p(i+1, j-1)时是回文,我们就不用在进行判断,只需要判断S[i] == s[j ]即可。从而减少时间复杂为O(n2), 空间复杂度为O(n2)(空间换时间思路)。
第三种思路是我们从头开始遍历,然后以此为中心考虑基数个数和偶数个数的时候,得出最长字符串的结果。这样复杂度为O(n2),空间复杂度为O(1)。
图示思路
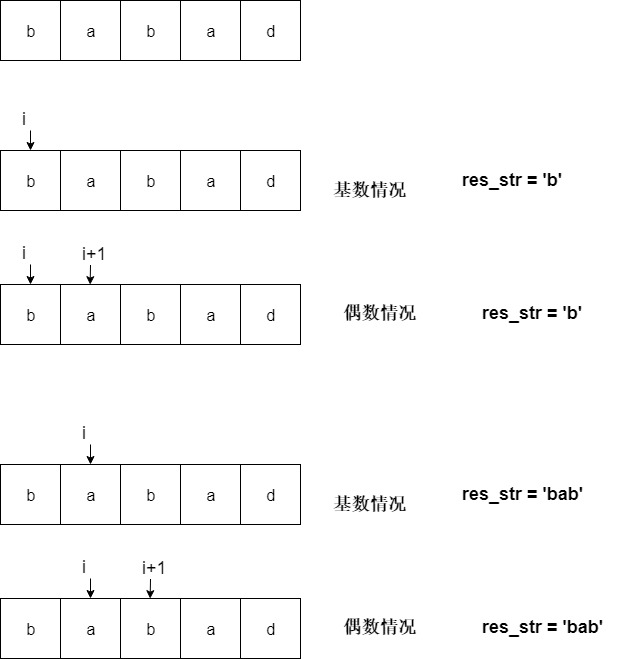
代码解决
1 class Solution(object):
2 def longestPalindrome(self, s):
3 """
4 :type s: str
5 :rtype: str
6 """
7 if len(s) < 2: # 长度小于2直接返回
8 return s
9 res_str = ''
10 for i in range(len(s)): # 从头开始遍历
11 tem = self.find_par(s, i, i) # 以基数的形式进行查找最长回文
12
13 if len(tem) > len(res_str): # 比较大小
14 res_str = tem
15
16 tem = self.find_par(s, i, i+1) # 以偶数形式进行查找
17 if len(tem) > len(res_str):
18 res_str = tem
19 return res_str # 返回结果
20
21 def find_par(self, s, start, end): # 查找函数
22 while start >=0 and end < len(s) and s[start] == s[end]: # 以当前小标为基准,前后移动,知道不相等或者前后超出范围为止。
23 start -= 1
24 end += 1
25 return s[start+1: end] # 返回结果字符串