[Luogu P1066] 2^k进制数 (组合数或DP)

 

题面

传送门：https://www.luogu.org/problemnew/show/P1066

---

Solution

这是一道神奇的题目，我们有两种方法来处理这个问题，一种是DP，一种是组合数。

这题需要高精度，以下省略此声明

.

如果你对数学不感兴趣/喜欢写DP/(不想虐待自己)，这里是DP做法。

首先，我们可以发现，这个数最多有w/k位(向上取整),如下图所示：

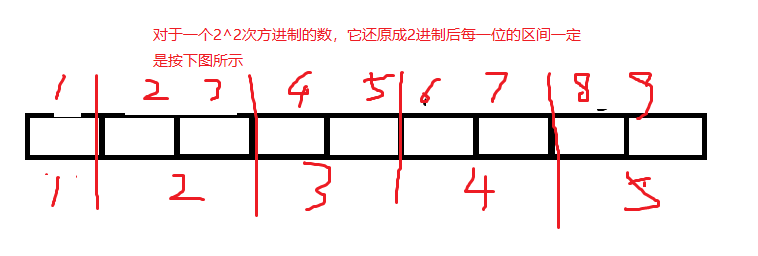
那么，我们就可以以这个特性做DP啦。

设f[i][j]表示枚举到第i位(指2^k进制下的)，最后一位数为j。

f[i][j] = ∑ f[i-1][k] ((j==0 and k==0) or k<j) 

这里的k显然是可以用前缀和优化的

初始化 f[1][i]=1 (i=0~2^(w%k)-1)

当然，还有一些小细节:f[倒数第2/第1个][0]=0

答案为∑f[w/k][i] 

（因为我没写过DP做法，这个做法纯口胡，如有错误请通知蒟蒻博主）

---

那....组合数呢？

事实上，这题的组合数做法的确很妙，（当然也有不少细节）

假设我们枚举了第一位数，那么后面位数的方案数是可以通过组合数来计算出来的。

因为后面的数要比第一位大，那么后面的数相当于从 [第一位数+1,2^k-1] 这个数的区间中选出x个数（x为后面的位数数量）来 （因为每一种方案都可以通过摆成升序满足题目要求）。

但是考虑到有可能有若干个前导零，我们还要枚举第一个位数从哪开始。

因为枚举了前导零，我们枚举第一位数时应该从1开始（从0开始会有重复）

这样子，答案为:

(事实上口胡起来简单，写起来还有很多细节，这得亲自体会然后就会感到这题的毒瘤)

就酱，我们就可以切掉嘴巴AC出这道题啦(～￣▽￣)～ 

---

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct Int128
{
    static const int N=500;
    int a[N],len;
    Int128()
    {
        memset(a,0,sizeof a);
        len=0;
    }
    void Print()
    {
        for(int i=len;i>=1;i--)
            printf("%d",a[i]);
    }
    friend Int128 operator * (Int128 A,int B)
    {
        for(int i=1;i<=A.len;i++)
            A.a[i]*=B;
        bool IsFullZero=true;
        for(int i=1;i<=A.len;i++)
        {
            if(A.a[i]>=10)
            {
                A.a[i+1]+=A.a[i]/10,A.a[i]%=10;
                if(i==A.len and A.a[i+1]!=0)
                    A.len++;
            }
            if(A.a[i]!=0) IsFullZero=false;
        }
        if(IsFullZero==true) A.len=1;
        return A;
    }
    friend Int128 operator / (Int128 A,int B)
    {
        Int128 ans;
        int temp=0;
        for(int i=A.len;i>=1;i--)
        {
            temp=temp*10+A.a[i];
            if(temp>=B)
            {
                ans.a[i]=temp/B,temp=temp%B;
                ans.len=max(ans.len,i);
            }
        }
        return ans;
    }
    friend Int128 operator + (Int128 A,Int128 B)
    {
        if(A.len<B.len) swap(A,B);
        for(int i=1;i<=A.len;i++)
        {
            A.a[i]=A.a[i]+B.a[i];
            if(A.a[i]>9)
            {
                A.a[i+1]++;A.a[i]-=10;
                if(i==A.len)
                    A.len++;
            }
        }
        return A;
    }
};
const int N=1<<(9+1);
Int128 C[N];
int n,x,K,w,first,m;
int main()
{
    scanf("%d%d",&K,&w);
    
    first=1<<(w%K),x=w/K;
    if(w%K==0) 
        first=1<<K,x--;
    m=1<<K;
    
    
    Int128 ans;
    for(int j=0;j<=x-1;j++)
    {
        int tx=x-j;
        memset(C[tx].a,0,sizeof C[tx].a);
        C[tx].a[1]=1,C[tx].len=1;
        for(int i=tx+1;i<=m;i++)
        {
            memset(C[i].a,0,sizeof C[i].a);
            C[i]=(C[i-1]*i)/(i-tx);
        }
        if(j!=0) first=m;
        for(int i=1;i<m and i<first;i++)
        {
            if(m-1-i<tx) break;
            ans=ans+C[m-1-i];
        }
        //ans.Print();
        //cerr<<endl;
    }
        
    ans.Print();
    return 0;
}