[Luogu P3626] [APIO2009] 会议中心

题面

传送门：https://www.luogu.org/problemnew/show/P3626

---

Solution

如果题目只要求求出第一问，那这题显然就是大水题。

但是加上第二问的话.......那这题就成为大（du）火（liu）题了。

对于第一问：求一整个区间的最大线段总数，我们可以很轻松的切掉。

怎么处理第二问呢？

我们可以考虑这样做：

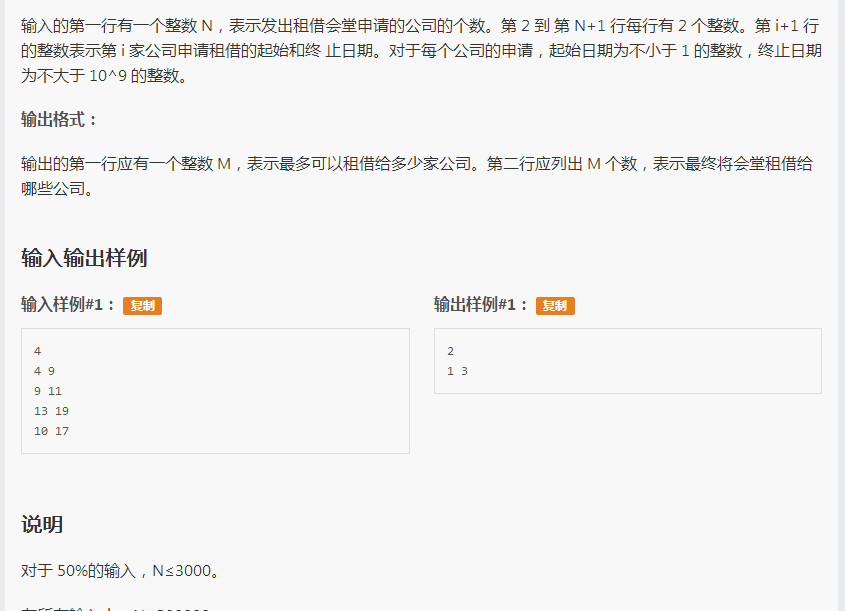
对于一条线段，如果它属于答案的一部分，那么它一定会有以下性质：

区间③的最大线段数 = 区间①的最大线段数 + 区间②的最大线段数 + 1（当前线段） （区间最大线段数指用传统贪心方法求出的一段区间的可能的最多的线段的数量）

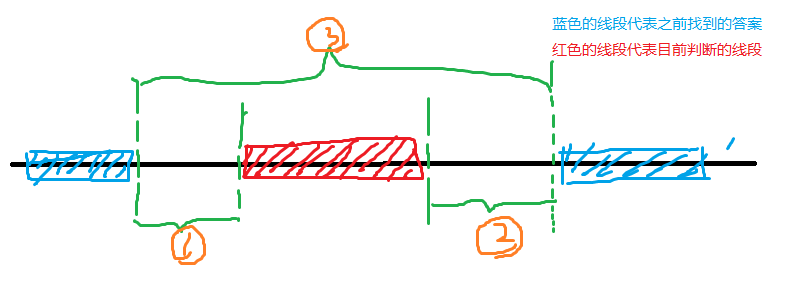
那怎么求一段区间的最大线段数呢？

第一想法是前缀和？看起来很OK？

nope

因为不同区间中，里面的的初始线段会不同，以下这个图可以简单说明这种情况

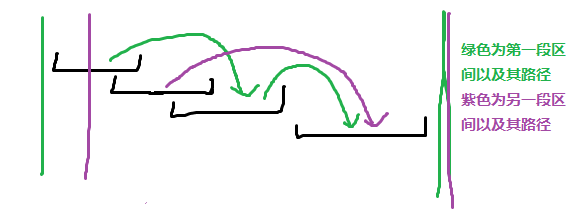
但是，我们可以发现一个很重要的特点：

每条线段的下一条可行线段是固定的

有了这个特点，我们就可以对路径做倍增，就可以在log的时间求出某一个区间的线段数。

至于求每一个区间的第一条线段，我们可以用set+lowbound的方法找。

这样子，你就可以嘴巴AC这道题啦

实际上你会花费大量的时间来调这道毒瘤题

---

（我常数太大，开O2才能卡过（set太辣鸡））

Code

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<set>
#include<stack>
#include<cstring>
#include<vector>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=200000+100;
struct line
{
    int l,r,no;
    friend bool operator < (line A,line B)
    {
        return A.l<B.l;
    }
}l[N];
bool cmp(line A,line B)
{
    if(A.l==B.l)
    {
        if(A.r!=B.r)
            return A.r>B.r;
        else
            return A.no>B.no;
    }
    return A.l<B.l;
}
bool cmp2(line A,line B)
{
    return A.no<B.no;
}
int n,ans,root,fa[N][20+2];
bool use[N],vis[N];
stack <int> ms;
set <line> mset;
set <line> used;
vector <int> e[N];
void dfs(int now,int FA)
{
    vis[now]=true;
    fa[now][0]=FA;
    for(int i=1;i<=20;i++)
        fa[now][i]=fa[fa[now][i-1]][i-1];
    for(int i=0;i<int(e[now].size());i++)
        if(vis[e[now][i]]==false)
            dfs(e[now][i],now);
}
int POW[21];
int Count(int L,int R)
{
    line temp; temp.l=L;
    set<line>:: iterator t=mset.lower_bound(temp);
    if((*t).r > R) return 0;
    int now=(*t).no,ans=1;
    for(int i=20;i>=0;i--)
        if(l[fa[now][i]].r<=R and fa[now][i]!=0)
            now=fa[now][i],ans+=POW[i];
    return ans;
}
int main()
{
    //freopen("center.in","r",stdin);
    //freopen("center.out","w",stdout);
    
    n=read();
    for(int i=1;i<=n;i++)
        l[i].l=read(),l[i].r=read(),l[i].no=i;
    
    sort(l+1,l+1+n,cmp);
    memset(use,1,sizeof use);
    for(int i=1;i<=n;i++)
    {
        while(ms.empty()==false and l[ms.top()].r>=l[i].r)
        {
            use[ms.top()]=false;
            ms.pop();
        }
        ms.push(i);
    }
    int to=-1;
    for(int i=1;i<=n;i++)
        if(use[i]==true and l[i].l>to)
        {
            ans++;
            to=l[i].r;
        }
    for(int i=1;i<=n;i++) e[i].reserve(4);
    for(int i=1;i<=n;i++)
        if(use[i]==true)
        {
            //cerr<<l[i].no<<" ";
            mset.insert(l[i]);
            bool OK=false;
            for(int j=i+1;j<=n;j++)
                if(use[j]==true and l[j].l>l[i].r)
                {
                    e[l[j].no].push_back(l[i].no);
                    OK=true;
                    break;
                }
            if(OK==false)
                e[0].push_back(l[i].no);
        }
    printf("%d
",ans);    
    
    dfs(0,0);
    sort(l+1,l+1+n,cmp2);
    for(int i=0;i<=20;i++)
        POW[i]=1<<i;
    l[0].r=0x3f3f3f3f;
    line tt;
    tt.l=-1,tt.r=-1,tt.no=0; mset.insert(tt),used.insert(tt);
    tt.l=0x3f3f3f3f,tt.r=0x3f3f3f3f;mset.insert(tt),used.insert(tt);
    for(int i=1;i<=n;i++)
    {
        int L,R;
        set<line>:: iterator t=used.lower_bound(l[i]);
        if((*t).l<=l[i].r) continue;
        R=(*t).l-1;
        t--;
        if((*t).r>=l[i].l) continue;
        L=(*t).r+1;
        if(Count(L,l[i].l-1)+Count(l[i].r+1,R)==Count(L,R)-1)
        {
            printf("%d ",i);
            used.insert(l[i]);
        }
    }
    return 0;
}