B. A Prosperous Lot
time limit per test1 second
memory limit per test256 megabytes
Problem Description
Apart from Nian, there is a daemon named Sui, which terrifies children and causes them to become sick. Parents give their children money wrapped in red packets and put them under the pillow, so that when Sui tries to approach them, it will be driven away by the fairies inside.
Big Banban is hesitating over the amount of money to give out. He considers loops to be lucky since it symbolizes unity and harmony.
He would like to find a positive integer n not greater than 1e18, such that there are exactly k loops in the decimal representation of n, or determine that such n does not exist.
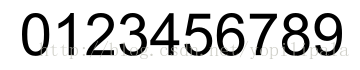
A loop is a planar area enclosed by lines in the digits’ decimal representation written in Arabic numerals. For example, there is one loop in digit 4, two loops in 8 and no loops in 5. Refer to the figure below for all exact forms.
Input
The first and only line contains an integer k (1 ≤ k ≤ 1e6) — the desired number of loops.
Output
Output an integer — if no such n exists, output -1; otherwise output any such n. In the latter case, your output should be a positive decimal integer not exceeding 1e18.
Examples
input
2
output
462
input
6
output
8080
解题心得:
- 题意看了好一会儿,其实就是一个数字,可能会形成封闭图形,输入n,叫你输出一个数字不超过1e18,在这个数字中有n个封闭图形,如果不能得到一个这样的数字就输出-1;
- 其实只要找到8和0来组织就行了,只有8能形成两个封闭图形,0能形成一个封闭图形还是最小的个位数,数字大小不超过1e18,所以最多能形成36个封闭图形,如果n大于36直接输出-1;
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
ll k;
scanf("%lld",&k);
if(k > 36){
printf("-1");
return 0;
}
int p = k/2;
for(int i=0;i<p;i++)
printf("8");
if(k%2)
printf("6");
return 0;
}