基础知识
复数表示
C = R + jI
极坐标:C = |C|(cosθ + jsinθ)
欧拉公式:C = |C|ejθ
有关更多的时域与复频域的知识可以学习复变函数与积分变换,本篇文章只给出DFT公式,性质,以及实现方法
二维离散傅里叶变换(DFT)
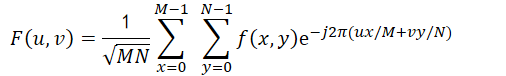
其中f(x,y)为原图像,F(u,v)为傅里叶变换以后的结果,根据欧拉公式可得,每个F(u,v)值都为复数,由实部和虚部组成
代码示例
1 void dft(short** in_array, double** re_array, double** im_array, long height, long width) 2 { 3 double re, im, temp; 4 5 for (int i = 0; i < height; i++){ 6 for (int j = 0; j < width; j++){ 7 re = 0; 8 im = 0; 9 10 for (int x = 0; x < height; x++){ 11 for (int y = 0; y < width; y++){ 12 temp = (double)i * x / (double)height + 13 (double)j * y / (double)width; 14 re += in_array[x][y] * cos(-2 * pi * temp); 15 im += in_array[x][y] * sin(-2 * pi * temp); 16 } 17 } 18 19 re_array[i][j] = re; 20 im_array[i][j] = im; 21 } 22 } 23 printf("dft done "); 24 }
傅里叶谱
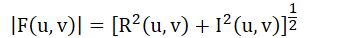
相角
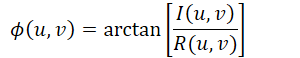
功率谱
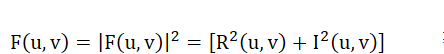
傅里叶变换频谱图


对于上面得两幅图案,在区间[0, M-1]中,变换数据由两个在点M/2处碰面的背靠背的半个周期组成
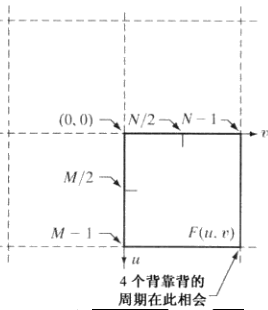
针对显示和滤波的目的,在该区间中有一个完整的变换周期更加方便,因为完整周期中数据是连续的

我们希望得到上图所示的图案
傅里叶变换的平移性质
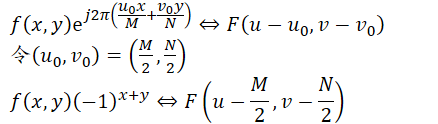
因此对每个f(x, y)项乘以(-1)x+y可达目的
代码示例
1 void fre_spectrum(short **in_array, short **out_array, long height, long width) 2 { 3 double re, im, temp; 4 int move; 5 6 for (int i = 0; i < height; i++){ 7 for (int j = 0; j < width; j++){ 8 re = 0; 9 im = 0; 10 11 for (int x = 0; x < height; x++){ 12 for (int y = 0; y < width; y++){ 13 temp = (double)i * x / (double)height + 14 (double)j * y / (double)width; 15 move = (x + y) % 2 == 0 ? 1 : -1; 16 re += in_array[x][y] * cos(-2 * pi * temp) * move; 17 im += in_array[x][y] * sin(-2 * pi * temp) * move; 18 } 19 } 20 21 out_array[i][j] = (short)(sqrt(re*re + im*im) / sqrt(width*height)); 22 if (out_array[i][j] > 0xff) 23 out_array[i][j] = 0xff; 24 else if (out_array[i][j] < 0) 25 out_array[i][j] = 0; 26 27 } 28 } 29 }
执行结果

旋转性质
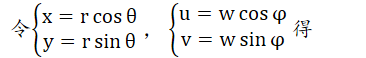
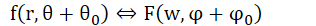
即f(x, y)旋转一个角度,F(u, v)旋转相同的角度

二维离散傅里叶反变换

代码示例
1 void idft(double** re_array, double** im_array, short** out_array, long height, long width) 2 { 3 double real, temp; 4 5 for (int i = 0; i < height; i++){ 6 for (int j = 0; j < width; j++){ 7 real = 0; 8 9 for (int x = 0; x < height; x++){ 10 for (int y = 0; y < width; y++){ 11 temp = (double)i * x / (double)height + 12 (double)j * y / (double)width; 13 14 real += re_array[x][y] * cos(2 * pi * temp) - 15 im_array[x][y] * sin(2 * pi * temp); 16 } 17 } 18 19 out_array[i][j] = (short)(real / sqrt(width*height)); 20 if (out_array[i][j] > 0xff) 21 out_array[i][j] = 0xff; 22 else if (out_array[i][j] < 0) 23 out_array[i][j] = 0; 24 } 25 } 26 printf("idft done "); 27 }
经验证,图像经傅里叶变换,然后再反变换以后可恢复原图
改进
本篇文章只是按照二维离散傅里叶变换公式进行了实现,在测试的过程中发现,执行速度真的是非常慢,算法时间复杂度O(n4),等以后有时间再对这段代码进行优化。
