Mysql索引深入理解

一.  引言

       Mysql 我们平常用的很多，了解的很多，今天别的不说，直接说mysql的底层是什么，说到底层，就想到数据结构，那么，mysql的数据结构是什么呢？ 是B + tree 。那么数据库中的索引是什么呢？

二.  索引是什么？

数据库的目的是为了存储数据，那么索引的概念是什么呢？ 最合理的解释,也是官方的解释就是：索引是帮助MySQL高效获取数据的数据结构。关键就是这个数据结构，什么目录的解释都是不合理的。

接下来我们去看看索引到底是如何高效获取数据的

先建一张student表简单的存放数据

id        name  

1         tom

2         jerry

3         jack

回到很久之前，大家先设想一下，如果之前没有mysql这种RDBMS(关系数据库管理系统)时，这些表存放在哪里呢？肯定是存放在文件之中。

那么，执行一个简单的查询，如 select  *   from   student   where   id  =  1;

如果要执行逐条筛选的话会特别慢，比如要找到 id =100的，就要筛选100条数据，显然是不合理的，那么索引究竟是如何高效获取数据的。

文件系统

首先，我们先看一下我们电脑中的文件系统，数据库数据是如何保存在文件中的

文件系统重要包括柱面 、 磁道和扇区，这是一种比较原始的存储方式

        

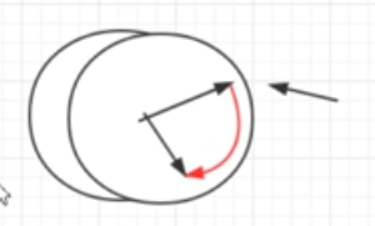
如图所示，如果每次查询都要从头转到尾的检索，效率性能都会很低，那么如果我们将id 与这条数据在扇区的位置记录（address）的对应记录起来的话，每次可以直接找到数据的位置，那么速率则会大大加快，如同我们看书时的目录一样，不需要讲前面的所有内容都过一遍。如下图所示：

到现在为止，我们已经对索引的概念和实现方式有了基本的认识 ，现在我们要谈论两个概念，一般存在于操作系统中，一个是时间局部性原理，一个是空间局部性原理。

时间局部性原理（Temporal Locality）：如果一个信息项正在被访问，那么在近期它很可能还会被再次访问。

程序循环、堆栈等是产生时间局部性的原因。

空间局部性原理（Spatial Locality）：在最近的将来将用到的信息很可能与现在正在使用的信息在空间地址上是临近的。

 

时间局部性原理和空间局部性原理打个比方就相当于快递员送快递一样，一般一个快递员只负责一片区域快递的配送，这个是空间局部性原理，这些快递一般都要在2个小时内送完，这是时间局部性原理。

为什么在索引中要去引入这两个概念呢？因为用索引去查询时，存在这种局部性的概念，比如执行语句   select  *   from   student   where   id  =  1;可能会在5分钟内再次调用该语句，这样我们就可以把该查询放入内存中去，这就是时间局部性原理。我们执行了id = 1 ，可能还会去执行 id= 2，id =3 这些语句，那么我们就去把这些类似查询的扇面全部查询一次，这就是空间局部性原理 （送快递不会一次只拿一个快递）。大家先大概了解一下这两个概念，我们继续往下走。

 

 

三.  为什么Mysql数据库要用B + tree 这种数据结构呢？

首先我们要先申明一个概念，判断索引的标准是什么？是IO渐进复杂度（就是IO执行的次数）

平时我们存放数据的数据结构有很多种，有hash，有红黑树等等，那么为什么我们要舍弃这些常用的数据结构而去用B + tree呢？我们依次去分析

 

Hash  hash(id)

用hash这种方式存储效率很高，通过key和value可以很快的获取到对应的值，那为什么我们不去用呢？因为当执行select  *   from   student   where   id  >  1; 这种sql的时候，hash就显得苍白无力了

 

在各种树的数据结构中，为什么不用普通的二叉树，为什么不用红黑树，而要用B+tree呢？我们从国外的一个网站上去清楚直观的去看一下各种数据结构，就可以知道为什么要使用B+tree了。

二叉树：

 

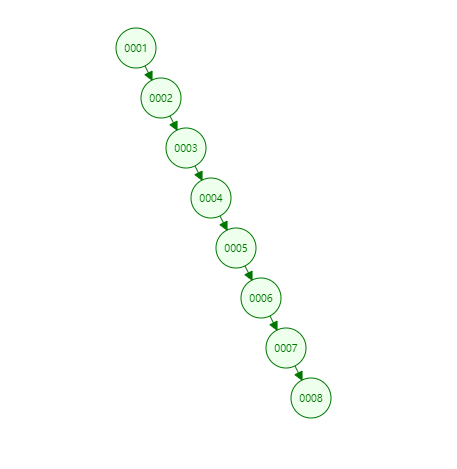
渐进复杂度是递增的！！！

二叉树是线性增加的，而且每个节点只能放一个数据，每查询一个数据，都会从头到尾执行一次，如果查询一次算一个IO的话，查询第1万条数据就要执行1万次IO，显然是不合理的。

红黑树：

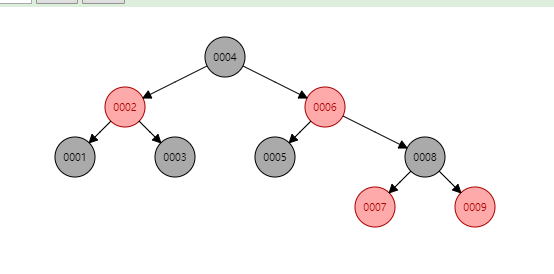
渐进复杂度是递增的！！！ 

虽然高度减少了，但是高度还是不可控的，IO执行次数还是过多

B + tree

 →       →      →    

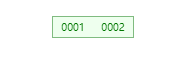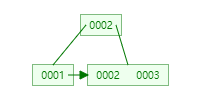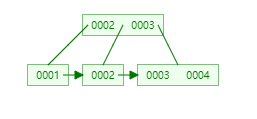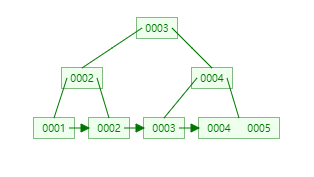
 在这里我们发现b+ tree的高度居然是不变的，大家看这些图，如果想查某一id 的值，只需要查两次，比如最后一张图，查id为1 的： 0003  ->  0002  ->0001 ,其余的也都是查两次，这样我们可以得到结论：

在B + Tree中，渐进复杂度是恒定不变的！！！

在B + Tree中，渐进复杂度是恒定不变的！！！

在B + Tree中，渐进复杂度是恒定不变的！！！

 重要的事说三遍