想了一个寻路算法,用C++实现了一下,界面用MFC完成的很简单。用20x20的方形区域作为迷宫,为了方便,随机选取了大约1/3的格子作为路障,禁止通过。规则是在只能想前后左右四个方向移动的前提下找到从入口(默认左上角)到出口(默认右下角)的最短路径。
源代码下载:https://files.cnblogs.com/GhostZCH/MFCMaze.rar(如果你下载了,希望你能留下只言片语,哪怕是“+1”也好,谢谢)
说来这个算法也不算难,借鉴了路由器建立路由表的算法,更加简化一些。熟悉TCP/IP协议的筒子们一定会记得路由表建立的原来,这个算法也一样,把每一个单元看成一个路由器,在它上下左右的四个格子可以看做与它联通的四个路由器。每个单元与相邻的单元交换路由信息,直到稳定下来,这样就获得了每个单元到出口的路由信息。所谓的路由信息并不是一条完整地路径,只保存了到达出口的跳数(距离)和下一跳(下一步)的位置。这样如果存在从入口到出口的路径就可以找出来。如果在与相邻单位交换信息时,只保存最短的路径,就可以得到最短路径,同时最短路选择也避免了绕圈形成死循环的问题。
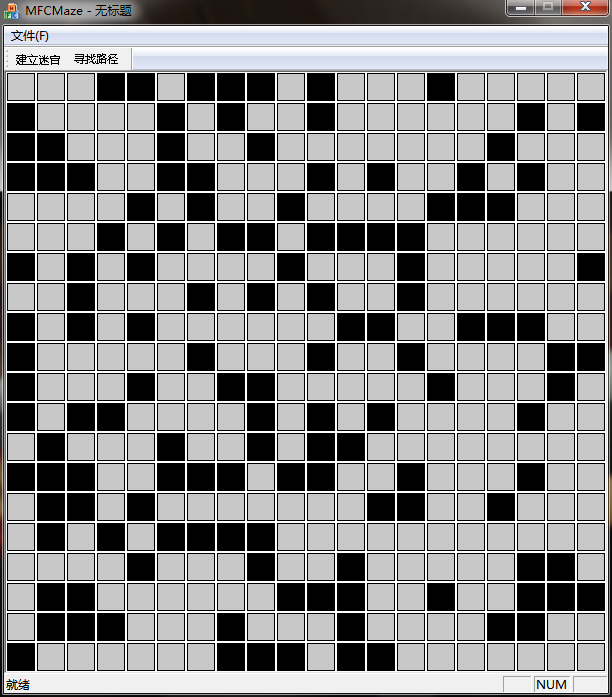


界面很简单,进入程序或者点击建立迷宫时生成一个随机迷宫,点击寻找路径后电脑会执行寻路算法,通过提示框提示寻路是否成功及迭代次数,如果成功显示路径和每个格子到出口的距离。黑色为障碍,灰色为可通过区域,绿色为电脑找到的路径,数字标明该格子到出口(右下角)的最短距离,没有数字的灰色格子说明这个格子与出口不连通。如上图中的左下区域。虽然结果只显示了从左上到右下的最短路径,事实上算法已经计算出每个格子(与出口联通的)到达出口的最短路径和距离。
下面的两组图片是生成的迷宫和找到的路径,运行时间没有计算,人工观测都小于1秒。有兴趣的筒子可以验证一下是不是最短的路径。






寻路的核心代码如下:
数据用的是“vector<Block *> _blocks”按照行优先的格式存下来的,在之前生成迷宫的时候就已经控制了入口和出口不是障碍,所以一开始先把出口的位置数据初始化了一下,剩下的就是迭代了。括号有十层,确实有点晕了,事实上不建议这样写代码的,超过五层括号就让人很迷惑了。但是考虑到程序本身比较小,既是不拆分函数也只有50行,不算变态(有一次需要读懂一个700行的函数,泪奔啊!!),循环体内部的逻辑也比较简单,没有太复杂的,所以就一个函数搞定,当然还是不建议大家这么做的。
1 int Grid::InitMap() 2 { 3 Block* target = _blocks.at(_height*_width-1); 4 target->CanReach(true); 5 target->JumpCount(0); 6 7 int times = 0; 8 bool ischanged = true; 9 //迭代到收敛,每个格子有最短个路径的长度和下一跳地址 10 while(ischanged) 11 { 12 times ++; 13 ischanged = false; 14 15 // 逐格闻讯周围格子路径 16 for (int i=0;i<_height;i++) 17 { 18 for (int j =0;j<_width;j++) 19 { 20 //问询邻居,选择最短的路径更新自己的路由信息 21 Block* block = Get(i,j); 22 if (block->CanPass()) 23 { 24 for (int ii=-1;ii<2;ii++)//-1到1 25 { 26 for (int jj=-1;jj<2;jj++)//-1到1 27 { 28 if(abs(ii)+abs(jj)==1)//只选四邻域 29 { 30 int x = i+ii; 31 int y = j+jj; 32 if (x>=0&&y>=0&&x<_height&&y<_width)//处于格子中的邻域 33 { 34 // 邻接格子中比自己路径短的更新自己的路径 35 Block *tmp = Get(x,y);//某个邻接的格子 36 if (tmp->CanReach()&&(tmp->JumpCount()+1)<block->JumpCount()) 37 { 38 block->CanReach(true);//设置可到达 39 block->JumpCount(tmp->JumpCount()+1);//设置跳数为邻近格子的跳数+1 40 block->NextJump(x*_width+y);//下一跳地址是邻接的格子 41 ischanged = true; 42 } 43 }//end if 44 }//end if 45 }//end for jj 46 }//end for ii 47 }//end if 48 }//end for j 49 }//end for i 50 }// end while 51 return times; 52 }
顺便多贴几张结果图,当然也有寻路失败的:




