NOI2011 Day2
道路修建
题目描述:给出一棵树,求每条边的两边的端点数的差乘边权之和。
solution:
题目可能描述得不太清楚,如图:

对于虚边,如果边权为10,两边的端点数之差为2,这条边对答案的贡献为20.
所以这道题就是求子树点数。
时间复杂度:(O(n))
NOI嘉年华
题目描述:给出(n)个活动,每个活动有起始时间和终止时间,把这(n)个活动分在两个会场进行(也可以不举行某些活动),每个会场的活动的时间段可以相交,两个会场的活动的时间段不可以有交集。求活动较少的会场的活动最大值,以及在第(i)个活动一定要举行的情况下,活动较少的会场的活动最大值。
solution:
因为有两个会场,所以其中一个会场的活动数通过枚举,再求另一个会场的活动最大值会比较方便。
设(f[i][j])表示到(i)时刻,A会场有(j)个活动,B会场活动数的最大值。(sum(i, j))为时刻(i)到时刻(j)所包含的活动数。那么:
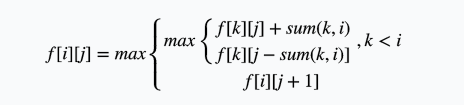
第一问的答案就是
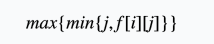
设(g[i][j])表示在第(i)时刻后,A会场有(j)个活动,B会场活动数的最大值。那么:

设(varphi [i][j])表示时刻(i)到时刻(j)包含的活动一定要举行,活动较少的会场的活动最大值。那么:

对于每一个活动,设起始时间为(L_i), 终止时间为(R_i),那么答案就是

对于固定的(i, j),设

当(x)增大时,如果(y)也增大, 那么左式(逗号左面)会增大,右式(逗号右面)会减少,因为是取最小值,所以贡献不大。
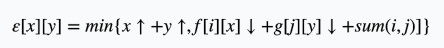
如果(y)减小,那么左式和右式都比较平衡,答案不会太差。

脑补……
时间复杂度:(O(n^3))
兔兔与蛋蛋游戏
题目描述:这个游戏是在一个 n 行 m 列的棋盘上进行的。游戏开始之前,棋盘上有一个格子是空的,其它的格子中都放置了一枚棋子,棋子或者是黑色,或者是白色。
每一局游戏总是兔兔先操作,之后双方轮流操作,具体操作为:
1、兔兔每次操作时,选择一枚与空格相邻的白色棋子,将它移进空格。
2、蛋蛋每次操作时,选择一枚与空格相邻的黑色棋子,将它移进空格。
第一个不能按照规则操作的人输掉游戏。
给出一局兔兔输的操作过程,找出犯错的地方:在这次操作前兔兔有必胜策略,而这次操作后蛋蛋有必胜策略。
solution:
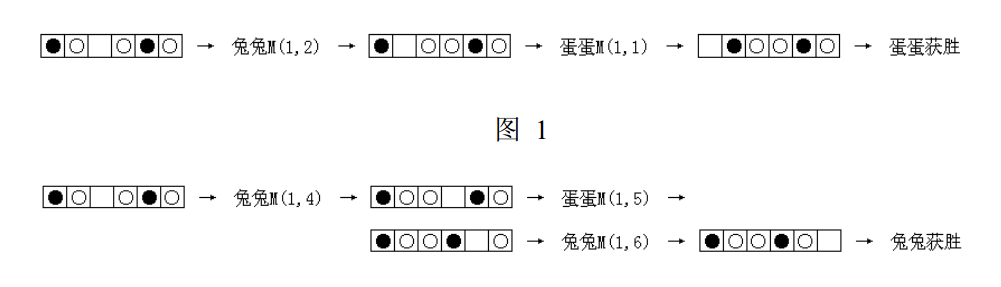
(M(x, y))表示哪个棋移到空格。
从操作可以看出:
1、路径不能自交(从某一个点出发走回这个点需要偶数步,第一步的颜色与偶数步的颜色不同,所以不可能自交)
2、如果把初始空格看做黑棋,则路径为一条黑白相间的路径。
由性质二可以按黑棋和白棋构成二分图(黑左白右),相邻的黑棋与白棋连边。
判断兔兔的某一步是否必胜,则需判断这一步的黑棋对应的点是否一定在最大匹配中,如果是,则必胜,否则必败。

如图(O)一定在最大匹配中,那么从(O)出发,一定是实虚相间的边,实边为匹配边,一定存在,而右边的点不一定有虚边回到左边,所以必胜。
如果像(P)一样不一定在最大匹配中,那么(P)会经虚边走到右边,而从右边一定会有实边走回左边,虚边不一定有,所以必败。
判断蛋蛋的某一步是否必胜,则需判断这一步的白棋对应的点是否能到达黑棋的一个必败态,如果是,则必胜,否则必败。
所以只要判断与该白棋相连的黑棋是否必胜即可。
判断某点是否在最大匹配中,只需做一次最大匹配,然后把该点删掉,再做一次最大匹配,判断两次的最大匹配是否相等即可。
因为每次只删一个点,所以只要重新匹配这个点相连的那个点就好了,不要再做一次最大匹配。
时间复杂度:(O(knm))